En Sección 1.9 presentamos el teorema de Gauss, que es que el componente normal total del flujo (D ) a través de una superficie cerrada es igual a la carga encerrada dentro de esa superficie. El teorema de Gauss es una consecuencia de la ley de Coulomb, en la que el campo eléctrico de una fuente puntual cae inversamente como el cuadrado de la distancia. Descubrimos que el teorema de Gauss era sorprendentemente útil, ya que nos permitía escribir casi de inmediato expresiones para el campo eléctrico en las proximidades de varias formas de cuerpos cargados sin pasar por muchos cálculos.
¿Existe quizás un teorema similar relacionado con el campo magnético alrededor de un conductor portador de corriente que nos permita calcular el campo magnético en su vecindad sin pasar por muchos cálculos? De hecho, existe, y se llama Teorema de Ampère .
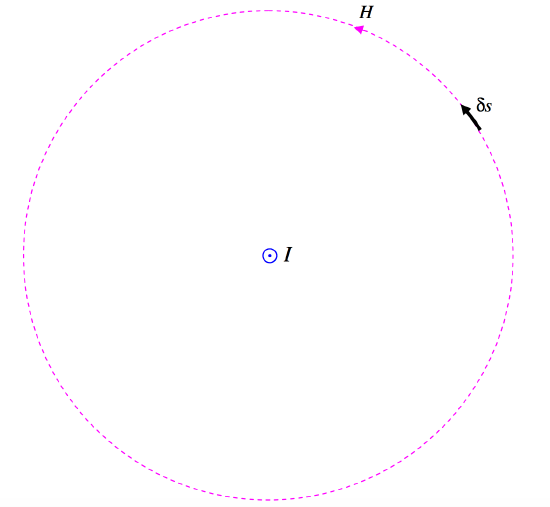
( text {FIGURE VI.9} )
En la figura ( text {VI.9} ) se supone que hay una corriente (I ) viniendo hacia ti en el medio del círculo. He dibujado una de las líneas de campo magnético: una línea discontinua de radio (r ). La fuerza del campo allí es (H = I / (2 pi r) ). También he dibujado una pequeña longitud elemental (ds ) en la circunferencia del círculo. La integral de línea del campo alrededor del círculo es solo (H ) veces la circunferencia del círculo. Es decir, la integral de línea del campo alrededor del círculo es solo (I ). Tenga en cuenta que esto es independiente del radio del círculo. A distancias mayores de la corriente, el campo cae como (1 / r ), pero la circunferencia del círculo aumenta como (r ), por lo que el producto de los dos (la integral de línea) es independiente de ( r ).
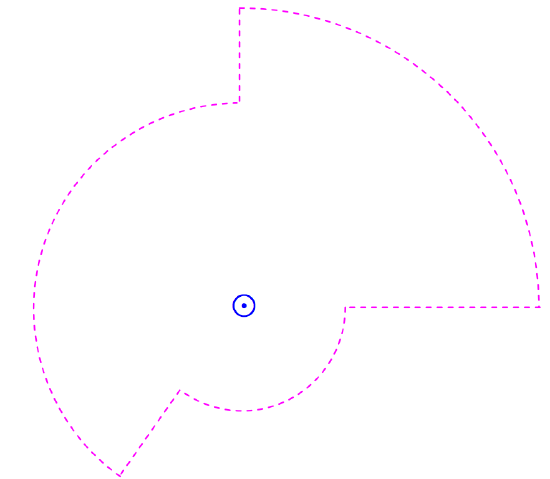
( text {FIGURE VI.10} )
En consecuencia, si calculo la integral de línea alrededor de un circuito como el que se muestra en la Figura ( text {VI.10} ), seguirá siendo solo (I ). De hecho, no importa cuál sea la forma del camino. La integral de línea es ( int textbf {H} cdot textbf {ds} ). El campo ( textbf {H} ) en algún punto es perpendicular a la línea que une la corriente al punto, y el vector ( textbf {ds} ) se dirige a lo largo del camino de integración, y ( textbf {H} cdot textbf {ds} ) es igual a (H ) veces el componente de ( textbf {ds} ) en la dirección de ( textbf {H} ), de modo que , independientemente de la longitud y la forma de la ruta de integración:
La integral de línea del campo ( textbf {H} ) alrededor de cualquier ruta cerrada es igual a la corriente encerrada por ese camino.
Este es Teorema de Ampère .
Así que ahora hagamos el solenoide infinito nuevamente. Calculemos la integral de la línea alrededor del camino amperiano rectangular que se muestra en la Figura ( text {VI.11} ). No hay contribución a la integral de línea a lo largo de los lados verticales del rectángulo porque estos lados son perpendiculares al campo, y no hay contribución desde el lado superior del rectángulo, ya que el campo es cero (si el solenoide es infinito) . La única contribución a la integral de la línea es a lo largo del lado inferior del rectángulo, y la integral de la línea es solo (Hl ), donde (l ) es la longitud del rectángulo. Si el número de vueltas de cable por unidad de longitud a lo largo del solenoide es (n ), habrá (nl ) vueltas encerradas por el rectángulo y, por lo tanto, la corriente encerrada por el rectángulo es (nlI ), donde (I ) es la corriente en el cable. Por lo tanto, según el teorema de Ampère, (Hl = nlI ), y así (H = nI ), que es lo que dedujimos antes de manera más laboriosa. Aquí (H ) es la intensidad del campo en la posición del lado inferior del rectángulo; pero podemos colocar el rectángulo a cualquier altura, por lo que vemos que el campo es (nI ) en cualquier lugar dentro del solenoide . Es decir, el campo dentro de un solenoide infinito es uniforme .
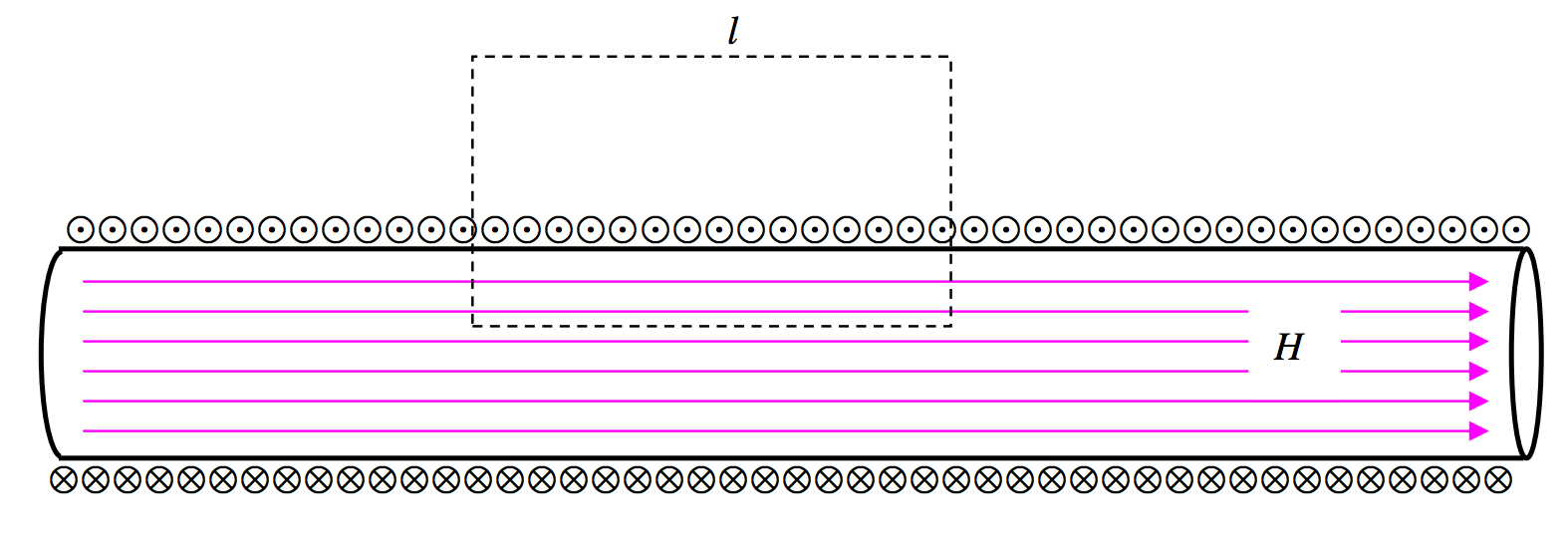
( text {FIGURA VI.11} )
Quizás valga la pena señalar que el teorema de Gauss es una consecuencia de la disminución cuadrada inversa del campo eléctrico con la distancia desde una carga puntual, y el teorema de Ampère es una consecuencia de la disminución inversa de la primera potencia del campo magnético con la distancia desde una corriente de línea.
Ejemplo ( PageIndex {1} )
Aquí hay un ejemplo del cálculo de una integral de línea (Figura ( text {VI.12} ))

Una corriente eléctrica (I ) fluye hacia el plano del papel en el origen de las coordenadas. Calcule la integral de línea del campo magnético a lo largo de la línea recta que une los puntos ((0, a) text {y} (a, a) ).
En la figura ( text {VI.13} ) dibujo una línea de fuerza (circular) del campo magnético ( textbf {H} ) y un vector ( textbf { dx} ) donde la línea de fuerza cruza la línea recta de interés.

La integral de línea a lo largo de la longitud elemental (dx ) es ( textbf {H} cdot textbf {dx} = H , dx , cos q ) . Aquí (H = frac {I} {2 pi (a ^ 2 + x ^ 2) ^ {1/2}} ) y ( cos theta = frac {a} {( a ^ 2 + x ^ 2) ^ {1/2}} ), por lo que la integral de línea a lo largo de ( textbf {dx} ) es ( frac {aI , dx} {2 pi (a ^ 2 + x ^ 2)} ). Integre esto desde (x = 0 text {to} x = a ) y encontrará que la respuesta es (I / 8 ).
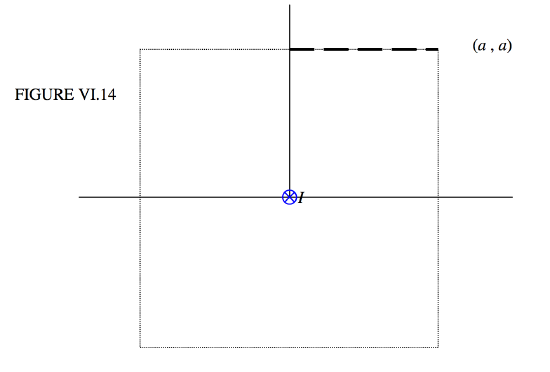
La figura ( text {VI.14} ) muestra otro método. La integral de línea alrededor del cuadrado es, según el teorema de Ampère, (I ), por lo que la integral de línea un octavo del recorrido es (I / 8 ).
Probablemente sentirá de inmediato que este segundo método es mucho mejor y muy “inteligente”. No lo niego, pero todavía vale la pena estudiar cuidadosamente el proceso de integración de líneas en el primer método.
Ejemplo ( PageIndex {2} )
Una corriente eléctrica (I ) fluye hacia el plano del papel. Calcule la integral de línea del campo magnético a lo largo de una línea recta de longitud (2a ) cuyo punto medio está a una distancia (a / sqrt {3} ) de la corriente.

Si no está acostumbrado a las integrales de línea, le recomiendo encarecidamente que lo haga por integración, como lo hicimos en El ejemplo anterior. Sin embargo, algunos lectores notarán que la línea es un lado de un triángulo equilátero, por lo que la línea integral a lo largo de la línea es solo ( frac {1} {3} I ).
Podemos jugar este juego con otros polígonos, por supuesto, pero resulta ser aún más fácil que eso.
Por ejemplo:

Muestre, por integración, que la integral de línea del campo magnético (H ) a lo largo de la línea gruesa es solo ( frac { theta} {2 pi} ) veces (I ).
Después de eso, no tardará mucho en convencerse de que la línea integral a lo largo de la línea gruesa en el dibujo a continuación también es ( frac { theta} {2 pi} ) veces (I ).
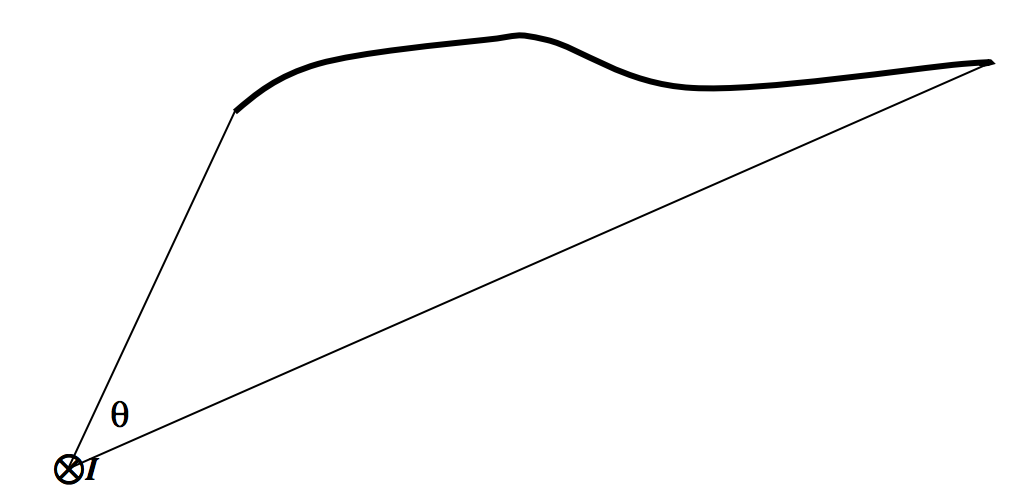
Ejemplo ( PageIndex {3} )
Una varilla metálica cilíndrica recta (o un cable) a lleva una corriente (I ). A una distancia (r ) del eje, el campo magnético es claramente (I / (2 pi r) text {if} r> a ). Pero, ¿cuál es el campo magnético dentro de la barra a una distancia r del eje, (r
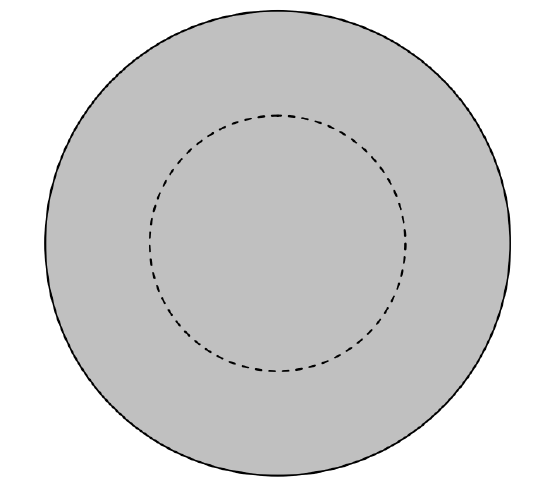
( text {FIGURE VI.15} )
Figure ( text {VI.15} ) muestra la sección transversal de la barra , y he dibujado un círculo amperiano de radio (r ). Si el campo en la circunferencia del círculo es (H ), la integral de línea alrededor del círculo es (2 pi rH ). La corriente encerrada dentro del círculo es (Ir ^ 2 / a ^ 2 ). Estos dos son iguales y, por lo tanto, (H = Ir / (2 pi a ^ 2) ).
En el ejemplo anterior, la densidad de corriente era uniforme. Pero ahora podemos pensar en muchos y muchos ejemplos en los que la densidad de corriente no es uniforme. Por ejemplo, imaginemos que tenemos un tubo cilíndrico largo y recto de radio (a ), quizás un acelerador lineal de partículas, y la densidad de corriente J (amperios por metro cuadrado) varía desde el medio (eje) del cilindro a su borde de acuerdo con (J (r) = J_0 (1-r / a) ). La corriente total es, por supuesto, (I = 2 pi int_0 ^ a J (r) r , dr = frac {1} {3} pi a ^ 2 J_0 ) y la densidad de corriente media es ( overline J = frac {1} {3} J_0 ).
La pregunta, sin embargo, es: ¿cuál es el campo magnético (H ) a una distancia (r ) del eje? Además, demuestre que el campo magnético en el borde (circunferencia) del cilindro es ( frac {1} {6} J_0 a ), y que el campo alcanza un valor máximo de ( frac {3} {16 } J_0 a ) en (r = frac {3} {4} a ).
Bueno, la corriente encerrada dentro de una distancia (r ) del eje es
[ nonumber I = 2 pi int_0 ^ r J (x) x , dx = pi J_0 r ^ 2 (1- frac {2r} {3a}), ]
y esto es igual a la integral de línea del campo magnético alrededor de un círculo de radio (r ) , que es (2 pi rH ). Así
[ nonumber H = frac {1} {2} J_0 r (1- frac {2r} {3a}). ]
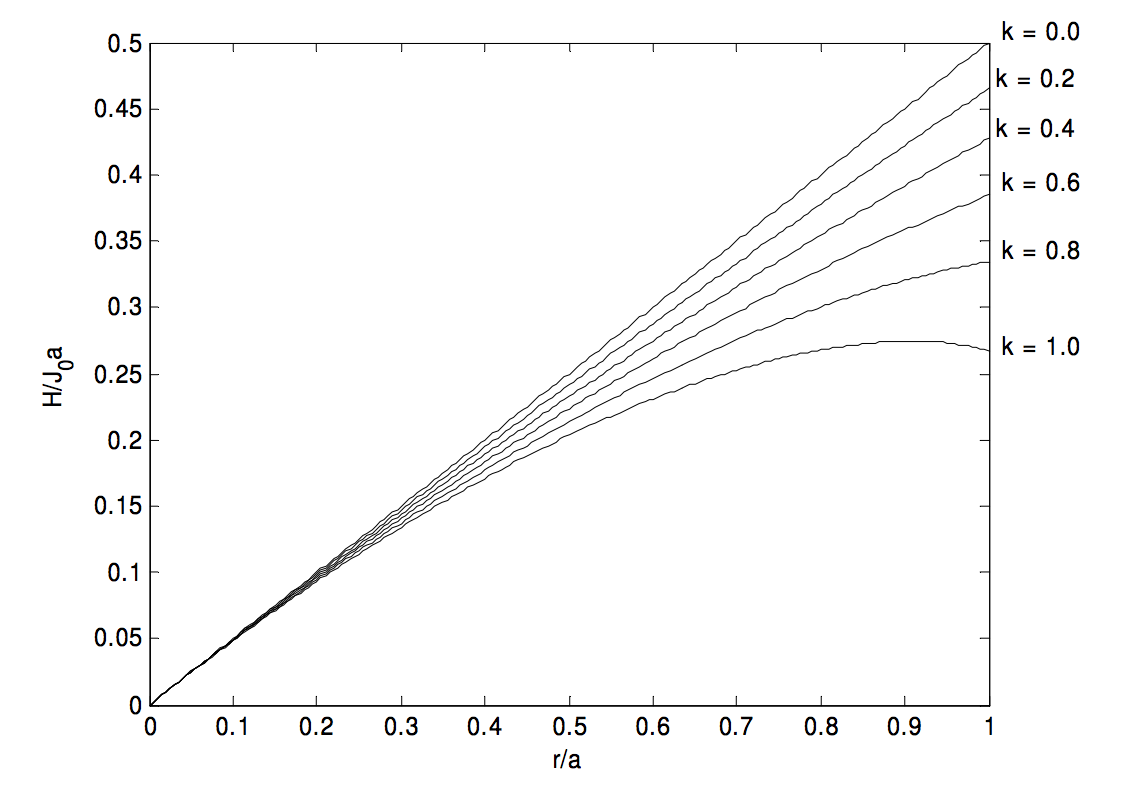
En la circunferencia del cilindro , esto viene a ( frac {1} {6} J_0 a ). El cálculo muestra que (H ) alcanza un valor máximo de ( frac {3} {16} J_0 a ) en (r = frac {3} {4} a ). El siguiente gráfico muestra (H / (J_0a) ) en función de (x / a ).
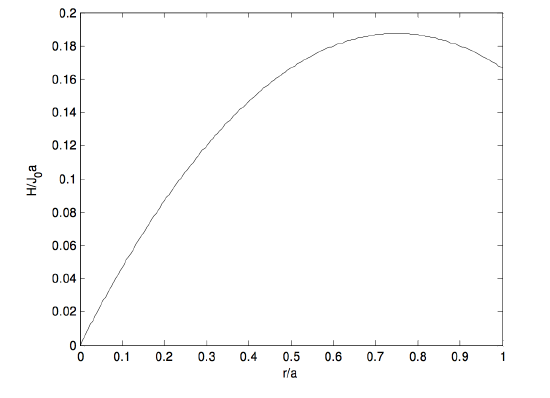
Habiendo despertado nuestros apetitos, ahora podemos intentar el mismo problema pero con algunas otras distribuciones de densidad de corriente, como
[ textbf {1 }: J (r) = J_0 left (1- frac {kr} {a} right); textbf {2}: J (r) = J_0 left (1- frac {kr ^ 2} {a ^ 2} right); textbf {3}: J (r) = J_0 sqrt {1- frac {kr} {a}}; textbf {4}: J (r) = J_0 sqrt {1- frac {kr ^ 2} {a ^ 2}}. nonumber ]
La densidad de corriente media es ( overline J = frac {2} {a ^ 2} int_0 ^ a rJ (r) , dr ), y la corriente total es ( pi a ^ 2 ) veces esto.
El campo magnético es (H (r) = frac {1} {r} int_0 ^ r xJ (x) , dx ).
Aquí están los resultados:
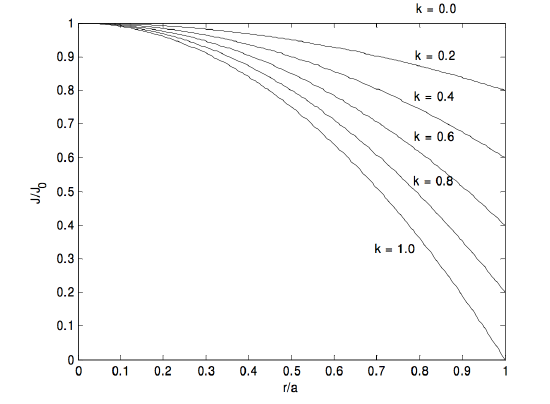
1. [J = J_0 left (1- frac {kr} {a} right), quad overline J = J_0 left (1- frac {2k} {3} right), quad H (r) = J_0 left ( frac {r} {2} – frac {kr ^ 2} {3a} right ). ]
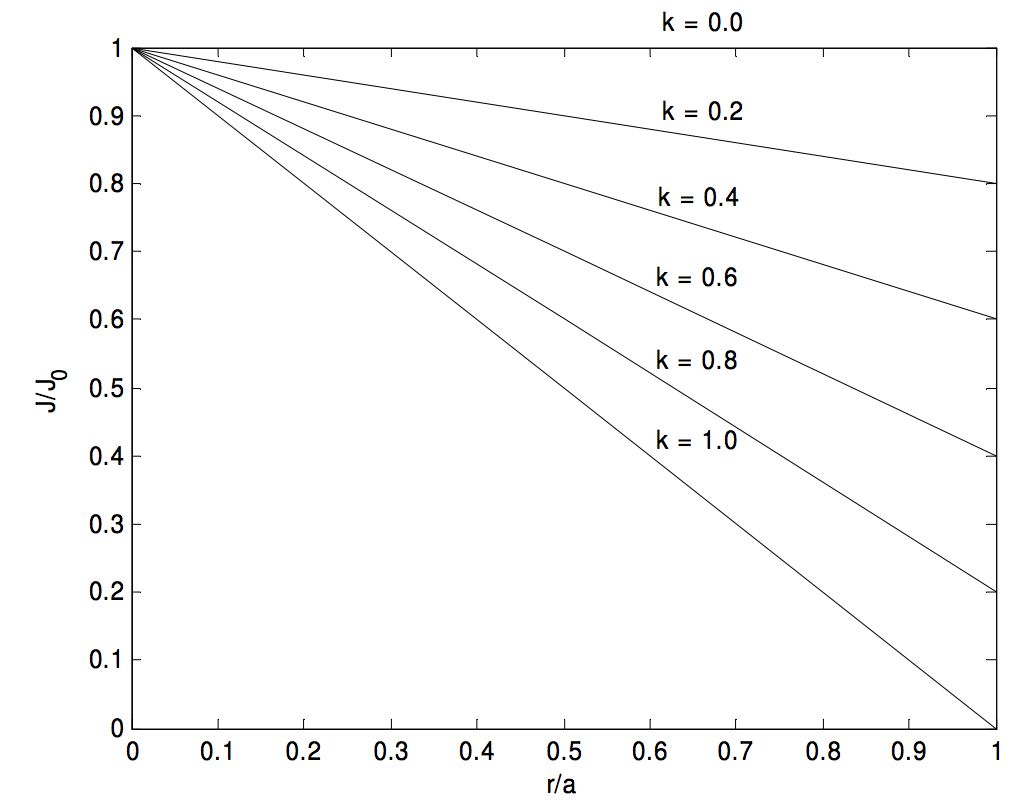
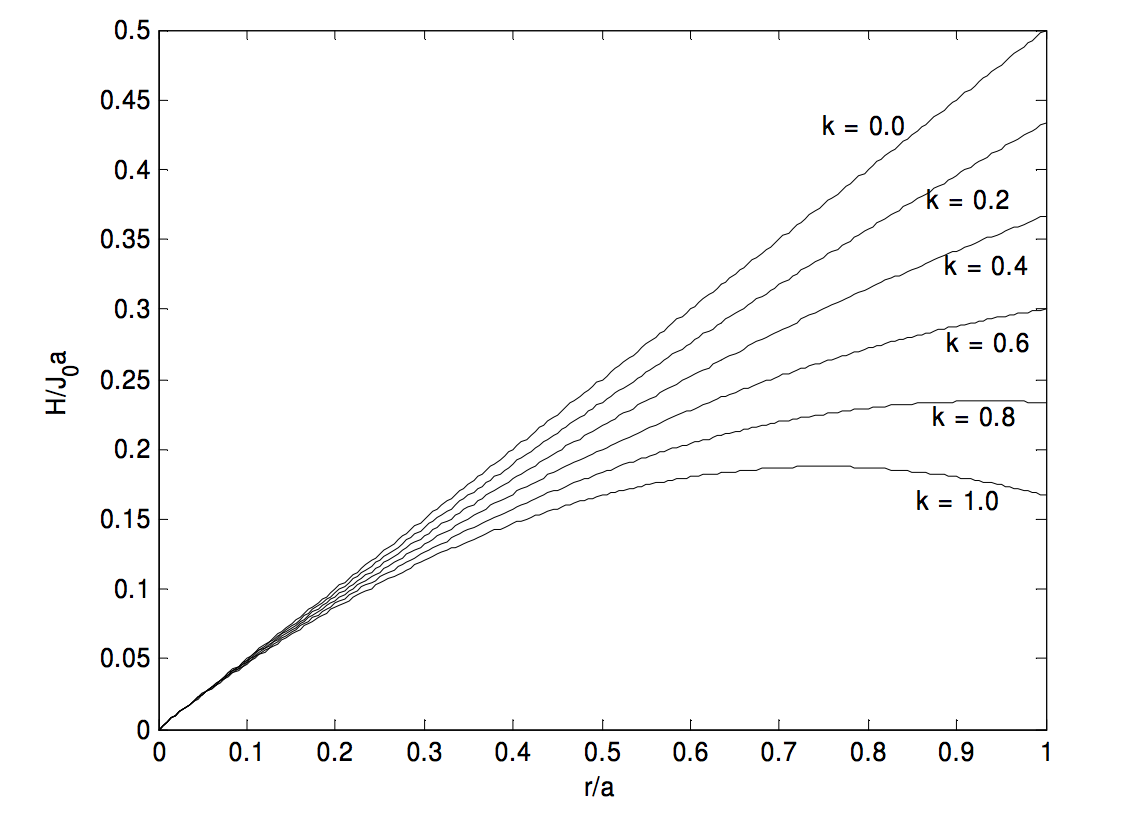
(H ) alcanza un valor máximo de ( frac {3J_0 a} {16k} text {at} r = frac {3a} {4k} ), pero este máximo ocurre dentro del cilindro solo si (k> frac {3} {4} ).
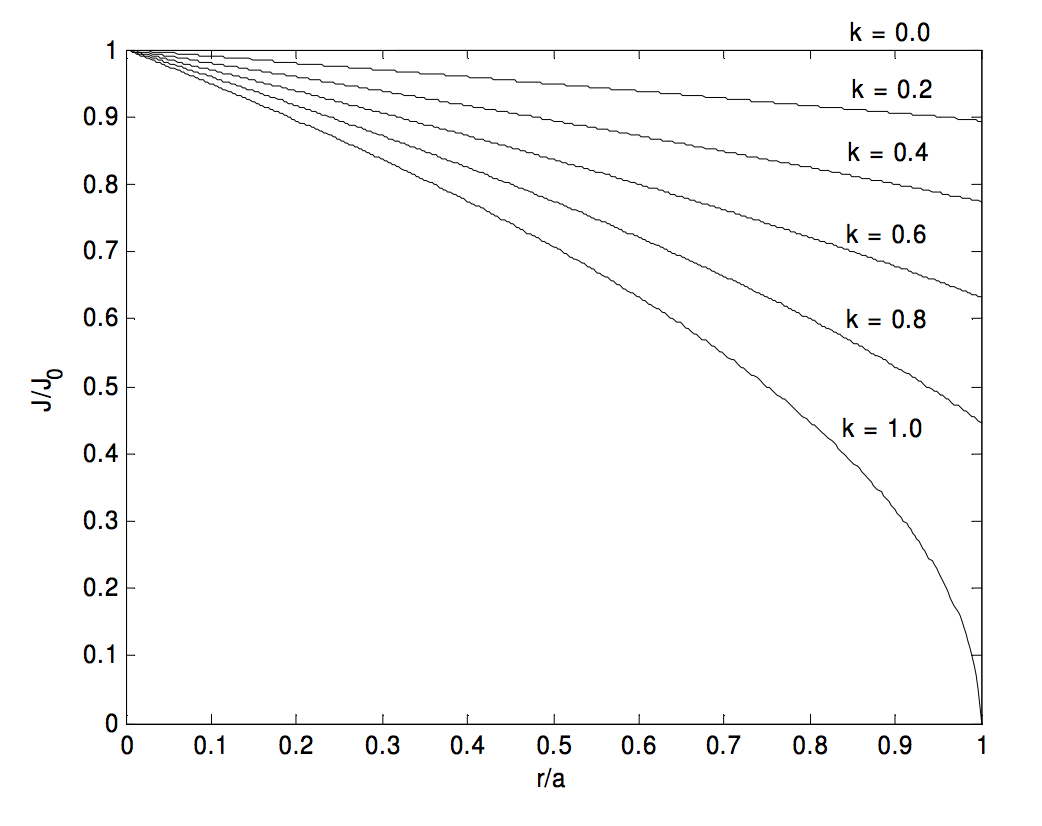
2. [J = J_0 left (1- frac {kr ^ 2} {a ^ 2} right), quad overline J = J_0 (1- frac { 1} {2} k), quad H (r) = J_0 left ( frac {r} {2} – frac {kr ^ 3} {4a ^ 2} right). ] [ 19459004]
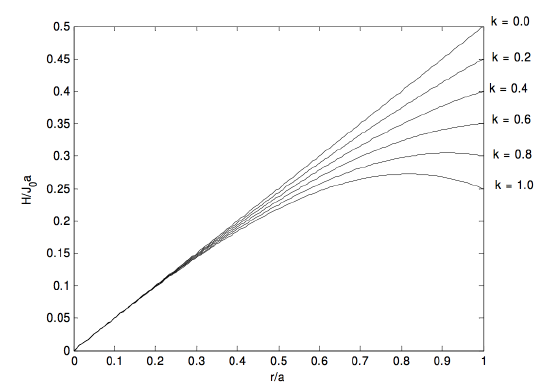
(H ) alcanza un valor máximo de ( sqrt { frac {2} {27k}} J_0 text {at} frac {r} {a} = sqrt { frac {2} {3k}} ), pero este máximo ocurre dentro del cilindro solo si (k> frac {2} {3} ) .
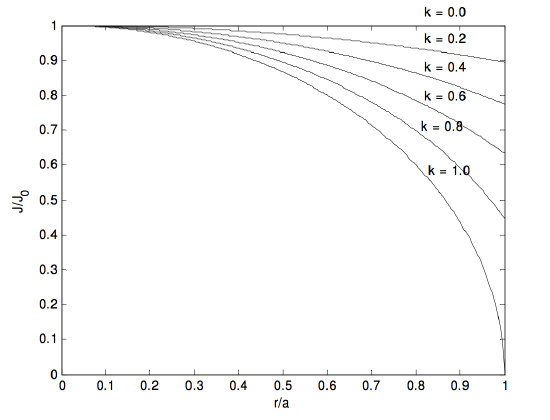
3. [J = J_0 sqrt {1- frac {kr} {a}}, quad overline J = frac {J_0} {15k ^ 2} [8- 20 (1-k) ^ {3/2} +12 (1-k) ^ {5/2}], quad H (r) = frac {2J_0 a ^ 2} {15k ^ 2r} left [ 2-5 left (1- frac {kr} {a} right) ^ {3/2} +3 left (1- frac {kr} {a} right) ^ {5/2} derecha]. ]
No he calculado fórmulas explícitas para las posiciones y valores de los máximos. Se produce un máximo dentro del cilindro si (k> 0.908901 ).
4. [J = J_0 sqrt {1- frac {kr ^ 2} {a ^ 2}}, quad overline J = frac {2J_0} {3k} left [1- (1-k) ^ {3/2} right], quad H (r) = frac {J_0 a ^ 2} {3kr} left [1- left (1- frac { kr ^ 2} {a ^ 2} right) ^ {3/2} right]. ]
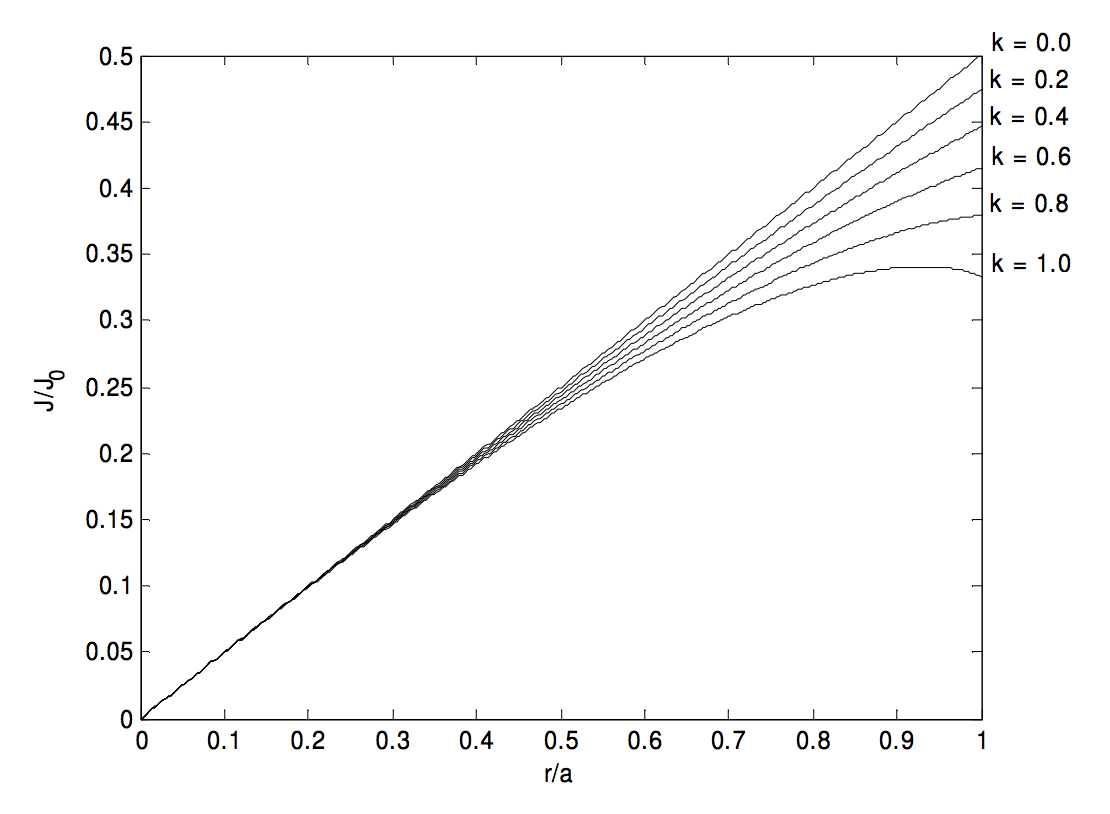
Un máximo ocurre dentro del cilindro si (k> 0.866025 ).
En todos estos casos, la condición de que no habrá un máximo (H ) dentro del cilindro, es decir, entre (r = 0 text {y} r = a ) [19459018 ] – es que ( frac {J (a)} { overline J}> frac {1} {2} ). Creo que esto es cierto para cualquier distribución de densidad de corriente axialmente simétrica, aunque no lo he probado. Espero que alguien interesado pueda encontrar una prueba bastante simple.
Las distribuciones de densidad de corriente adicionales que los lectores pueden desear investigar son
[J = frac {J_0} {1 + x / a} qquad J = frac {J_0} {1 + x ^ 2 / a ^ 2} qquad J = frac {J_0} { sqrt {1 + x / a}} nonumber ]
[J = frac {J_0} { sqrt {1 + x ^ 2 / a ^ 2}} qquad J = J_0e ^ {- x / a} qquad J = J_0 e ^ {- x ^ 2 / a ^ 2} nonumber ]
[ 19459021]