Una de las características más llamativas de los complejos de metales de transición es la amplia gama de colores que exhiben. En esta sección, describimos la teoría del campo de cristal (CFT), un modelo de enlace que explica muchas propiedades importantes de los complejos de metales de transición, incluidos sus colores, magnetismo, estructuras, estabilidad y reactividad. La suposición central de CFT es que las interacciones metal-ligando son de naturaleza puramente electrostática. Aunque esta suposición claramente no es válida para muchos complejos, como los que contienen ligandos neutros como el CO, CFT permite a los químicos explicar muchas de las propiedades de los complejos de metales de transición con un grado razonable de precisión. El objetivo de aprendizaje de este módulo es comprender cómo la teoría del campo cristalino explica las estructuras electrónicas y los colores de los complejos metálicos.
D-Orbital Splittings
CFT se centra en la interacción de los cinco (n – 1) d orbitales con ligandos dispuestos en una matriz regular alrededor de un ion de metal de transición. Nos centraremos en la aplicación de CFT a complejos octaédricos, que son, con mucho, los más comunes y los más fáciles de visualizar. Otras estructuras comunes, como los complejos planos cuadrados, pueden tratarse como una distorsión del modelo octaédrico. Según CFT, se forma un complejo metálico octaédrico debido a la interacción electrostática de un ion metálico cargado positivamente con seis ligandos cargados negativamente o con los extremos negativos de dipolos asociados con los seis ligandos. Además, los ligandos interactúan entre sí electrostáticamente. Como aprendió en nuestra discusión sobre el modelo de repulsión de pares de electrones de capa de valencia (VSEPR), la disposición de energía más baja de seis cargas negativas idénticas es un octaedro, que minimiza las interacciones repulsivas entre los ligandos.
Comenzamos considerando cómo las energías de los orbitales d de un ion de metal de transición se ven afectadas por una disposición octaédrica de seis cargas negativas. Recuerde que los cinco orbitales d están inicialmente degenerados (tienen la misma energía). Si distribuimos seis cargas negativas uniformemente sobre la superficie de una esfera, los orbitales d permanecen degenerados, pero su energía será mayor debido a las interacciones electrostáticas repulsivas entre la capa esférica de carga negativa y los electrones en los orbitales d (Figura ( PageIndex {1a} )). Colocar las seis cargas negativas en los vértices de un octaedro no cambia la energía promedio de los orbitales d, pero elimina su degeneración: los cinco orbitales se dividen en dos grupos cuyas energías dependen de sus orientaciones. Como se muestra en la Figura ( PageIndex {1b} ), la d z 2 yd x 2 −y 2 [ 19459017] los orbitales apuntan directamente a las seis cargas negativas ubicadas en los ejes x, y y z. En consecuencia, la energía de un electrón en estos dos orbitales (denominados colectivamente los orbitales e g ) será mayor de lo que será para una distribución esférica de carga negativa debido al aumento de las repulsiones electrostáticas. En contraste, los otros tres orbitales d (d xy , d xz yd yz , colectivamente llamados orbitales t 2g ) Todos están orientados en un ángulo de 45 ° con respecto a los ejes de coordenadas, por lo que apuntan entre las seis cargas negativas. La energía de un electrón en cualquiera de estos tres orbitales es menor que la energía para una distribución esférica de carga negativa.
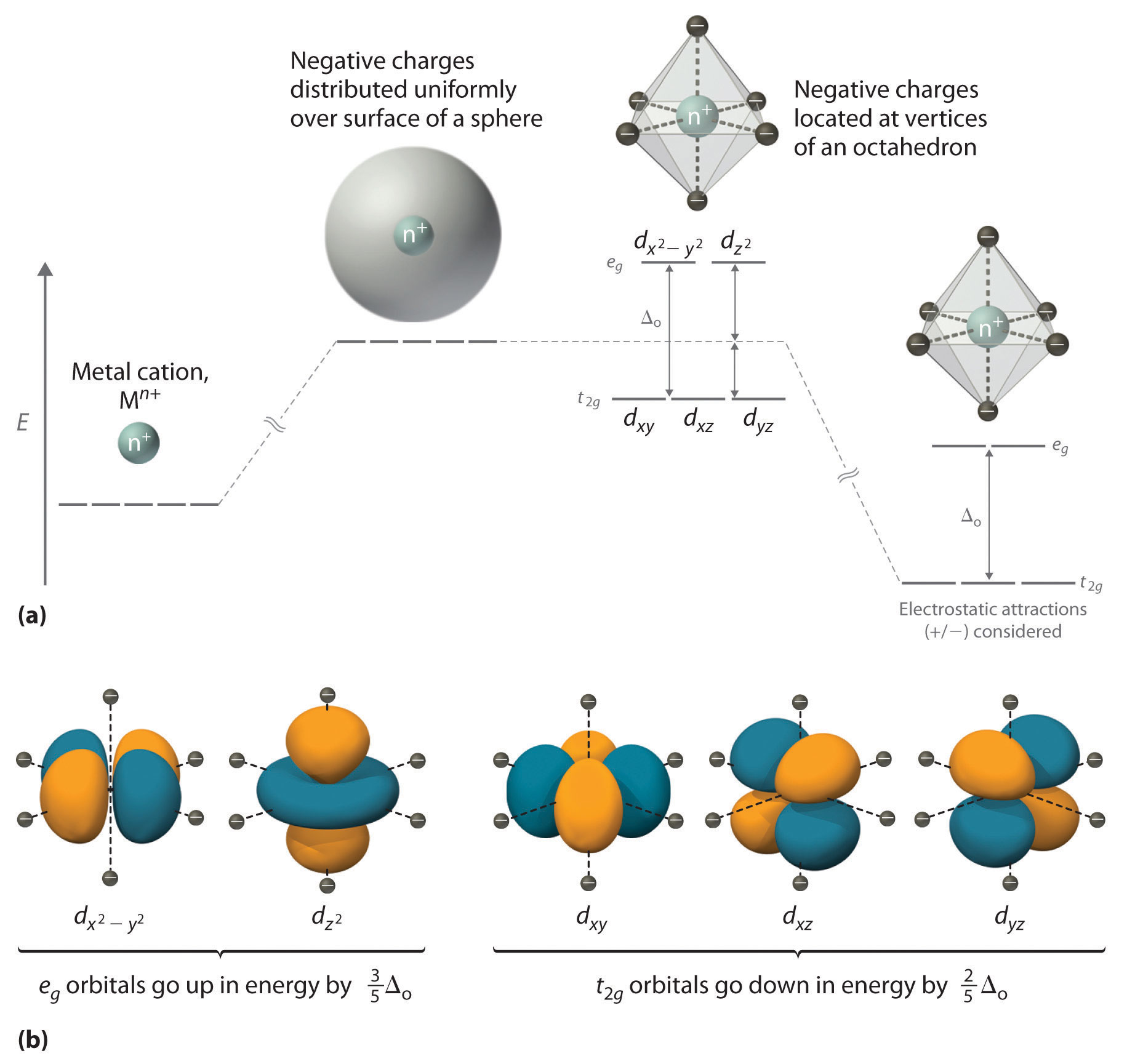
La diferencia de energía entre los dos conjuntos de d orbitales se denomina energía de división del campo cristalino (Δ o ), donde el subíndice o representa octaédrico. Como veremos, la magnitud de la división depende de la carga del ion metálico, la posición del metal en la tabla periódica y la naturaleza de los ligandos. (La energía de división del campo de cristal también se aplica a los complejos tetraédricos: Δ t .) Es importante tener en cuenta que la división de los orbitales d en un campo de cristal no cambia la energía total de los cinco orbitales d: dos orbitales e g aumentan en energía en 0.6Δ o , mientras que los tres t 2g orbitales disminuyen en energía en 0.4Δ o . Por lo tanto, el cambio total en la energía es
[2 (0.6Δ_o) + 3 (−0.4Δ_o) = 0. ]
La división del campo de cristal no cambia la energía total de los orbitales d.
Hasta ahora, solo hemos considerado el efecto de las interacciones electrostáticas repulsivas entre los electrones en los orbitales d y los seis ligandos cargados negativamente, lo que aumenta la energía total del sistema y divide los d orbitales. Las interacciones entre el ion metálico cargado positivamente y los ligandos dan como resultado una estabilización neta del sistema, lo que disminuye la energía de los cinco orbitales d sin afectar su división (como se muestra en el extremo derecho en la Figura ( PageIndex {1a} ) )
Estructuras electrónicas de complejos metálicos
Podemos usar el diagrama de nivel de energía d-orbital en la Figura ( PageIndex {1} ) para predecir estructuras electrónicas y algunas de las propiedades de los complejos de metales de transición. Comenzamos con el ion Ti 3 + , que contiene un solo electrón d, y avanzamos a través de la primera fila de los metales de transición agregando un solo electrón a la vez. Colocamos electrones adicionales en el orbital de energía más baja disponible, mientras mantenemos sus giros paralelos como lo requiere la regla de Hund. Como se muestra en la figura 24.6.2, para los sistemas d 1 –d 3 , como [Ti (H 2 O) 6 ] 3+ , [V (H 2 O) 6 ] 3+ y [Cr (H 2 [ 19459018] O) 6 ] 3+ , respectivamente — los electrones ocupan sucesivamente los tres orbitales t degenerados 2g con sus espines paralelos, dando uno, dos y tres electrones no apareados, respectivamente. Podemos resumir esto para el complejo [Cr (H 2 O) 6 ] 3+ , por ejemplo, diciendo que el ion cromo tiene ad [19459016 ] 3 configuración electrónica o, más sucintamente, Cr 3 + es un ión 3 .
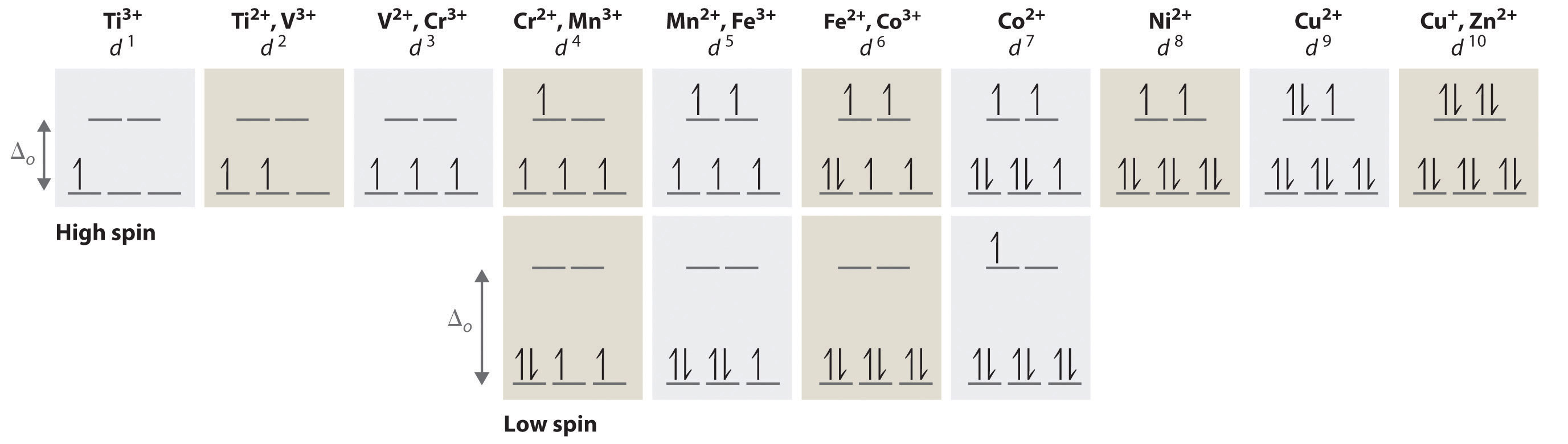
Cuando alcanzamos la configuración d 4 , hay dos opciones posibles para el cuarto electrón: puede ocupar uno de los orbitales e g vacío o uno de los ocupados individualmente t 2g orbitales. Recuerde que colocar un electrón en un orbital ya ocupado produce repulsiones electrostáticas que aumentan la energía del sistema; Este aumento de energía se denomina energía de emparejamiento de giro (P) . Si Δ o es menor que P, entonces la disposición de energía más baja tiene el cuarto electrón en uno de los orbitales e g vacíos. Debido a que esta disposición da como resultado cuatro electrones no apareados, se denomina configuración de alto espín y complejo con esta configuración de electrones, como [Cr (H 2 O) 6 ] 2+ ion, se llama complejo de alto spin. Por el contrario, si Δ o es mayor que P, entonces la disposición de energía más baja tiene el cuarto electrón en uno de los orbitales t 2g ocupados. Debido a que esta disposición da como resultado solo dos electrones no apareados, se denomina configuración de bajo giro y complejo con esta configuración electrónica, como [Mn (CN) 6 ] 3− [19459017 ] ion, se llama complejo de baja rotación. De manera similar, los iones metálicos con las configuraciones electrónicas d 5 , d 6 o d 7 pueden ser de alto o bajo giro, dependiendo de la magnitud de Δ o .
En contraste, solo una disposición de electrones d es posible para iones metálicos con configuraciones de electrones d 8 –d 10 . Por ejemplo, el ión [Ni (H 2 O) 6 ] 2+ es d 8 con dos electrones no apareados, el [ Cu (H 2 O) 6 ] 2+ el ion es d 9 con un electrón no apareado, y el [Zn (H [ 19459015] 2 O) 6 ] 2+ el ion es d 10 sin electrones no apareados.
Si Δ o es menor que la energía de emparejamiento de espín, se obtiene una configuración de alto espín. Por el contrario, si Δ o es mayor, se forma una configuración de giro bajo.
Factores que afectan la magnitud de Δ o
La magnitud de Δ o dicta si un complejo con cuatro, cinco, seis o siete electrones d es alto o bajo, lo que afecta sus propiedades magnéticas, estructura y reactividad. Los valores grandes de Δ o (es decir, Δ o > P) producen un complejo de giro bajo, mientras que los valores pequeños de Δ o (es decir, Δ ] o
| Complejos octaédricos | Δ o (cm −1 ) | Complejos octaédricos | Δ o (cm −1 ) | Complejos tetraédricos | Δ t (cm −1 ) |
|---|---|---|---|---|---|
| * Las energías obtenidas por mediciones espectroscópicas a menudo se dan en unidades de números de onda (cm −1 ); el número de onda es el recíproco de la longitud de onda de la correspondiente radiación electromagnética expresada en centímetros: 1 cm −1 = 11,96 J / mol. | |||||
| [Ti (H 2 O) 6 ] 3+ | 20,300 | [Fe (CN) 6 ] 4− | 32,800 | VCl 4 | 9010 |
| [V (H 2 O) 6 ] 2+ | 12,600 | [Fe (CN) 6 ] 3− | 35,000 | [CoCl 4 ] 2− | 3300 |
| [V (H 2 O) 6 ] 3+ | 18,900 | [CoF 6 ] 3− | 13,000 | [CoBr 4 ] 2− | 2900 |
| [CrCl 6 ] 3− | 13,000 | [Co (H 2 O) 6 ] 2+ | 9300 | [CoI 4 ] 2− | 2700 |
| [Cr (H 2 O) 6 ] 2+ | 13,900 | [Co (H 2 O) 6 ] 3+ | 27,000 | ||
| [Cr (H 2 O) 6 ] 3+ | 17.400 | [Co (NH 3 ) 6 ] 3+ | 22,900 | ||
| [Cr (NH 3 ) 6 ] 3+ | 21,500 | [Co (CN) 6 ] 3− | 34,800 | ||
| [Cr (CN) 6 ] 3− | 26,600 | [Ni (H 2 O) 6 ] 2+ | 8500 | ||
| Cr (CO) 6 | 34,150 | [Ni (NH 3 ) 6 ] 2+ | 10,800 | ||
| [MnCl 6 ] 4− | 7500 | [RhCl 6 ] 3− | 20,400 | ||
| [Mn (H 2 O) 6 ] 2+ | 8500 | [Rh (H 2 O) 6 ] 3+ | 27,000 | ||
| [MnCl 6 ] 3− | 20,000 | [Rh (NH 3 ) 6 ] 3+ | 34,000 | ||
| [Mn (H 2 O) 6 ] 3+ | 21,000 | [Rh (CN) 6 ] 3− | 45,500 | ||
| [Fe (H 2 O) 6 ] 2+ | 10,400 | [IrCl 6 ] 3− | 25,000 | ||
| [Fe (H 2 O) 6 ] 3+ | 14.300 | [Ir (NH 3 ) 6 ] 3+ | 41,000 | ||
Fuente de datos: Duward F. Shriver, Peter W. Atkins y Cooper H. Langford, Inorganic Chemistry, 2ª ed. (Nueva York: W. H. Freeman and Company, 1994).
Carga sobre el ion de metal
El aumento de la carga en un ion metálico tiene dos efectos: el radio del ion metálico disminuye y los ligandos cargados negativamente se sienten más atraídos por él. Ambos factores disminuyen la distancia metal-ligando, lo que a su vez hace que los ligandos con carga negativa interactúen más fuertemente con los orbitales d. En consecuencia, la magnitud de Δ o aumenta a medida que aumenta la carga en el ion metálico. Típicamente, Δ o para un ion tripositivo es aproximadamente un 50% mayor que para el ion dipositivo del mismo metal; por ejemplo, para [V (H 2 O) 6 ] 2+ , Δ o = 11,800 cm −1 ; para [V (H 2 O) 6 ] 3+ , Δ o = 17,850 cm −1 .
Número cuántico principal del metal
Para una serie de complejos de metales del mismo grupo en la tabla periódica con la misma carga y los mismos ligandos, la magnitud de Δ o aumenta al aumentar el número cuántico principal: Δ o (3d) <Δ o (4d) <Δ o (5d). Los datos para los complejos de hexaammina de los metales del grupo 9 trivalente ilustran este punto:
[Co (NH 3 ) 6 ] 3+ : Δ o = 22,900 cm −1 [19459017 ]
[Rh (NH 3 ) 6 ] 3+ : Δ o = 34,100 cm −1 [19459017 ]
[Ir (NH 3 ) 6 ] 3+ : Δ o = 40,000 cm −1 [19459017 ]
El aumento de Δ o con el aumento del número cuántico principal se debe al mayor radio de los orbitales de valencia hacia abajo de una columna. Además, las interacciones repulsivas ligando-ligando son más importantes para los iones metálicos más pequeños. Relativamente hablando, esto resulta en distancias M-L más cortas e interacciones d orbitales-ligando más fuertes.
La naturaleza de los ligandos
Experimentalmente, se encuentra que el Δ o observado para una serie de complejos del mismo ion metálico depende en gran medida de la naturaleza de los ligandos. Para una serie de ligandos químicamente similares, la magnitud de Δ o disminuye a medida que aumenta el tamaño del átomo donante. Por ejemplo, los valores de Δ o para complejos de haluros generalmente disminuyen en el orden F – > Cl – > Br – > I− porque cargas más pequeñas y localizadas, como vemos para F – , interactúan más fuertemente con los orbitales d del ion metálico. Además, un ligando neutro pequeño con un par solitario altamente localizado, como NH 3 , da como resultado valores de Δ o significativamente mayores de lo que cabría esperar. Debido a que el par solitario apunta directamente al ion metálico, la densidad electrónica a lo largo del eje M – L es mayor que para un anión esférico como F – . El orden observado experimentalmente de las energías de división del campo cristalino producidas por diferentes ligandos se denomina serie espectroquímica, que se muestra aquí en orden decreciente Δ o :
( mathrm { underset { textrm {ligandos de campo fuerte}} {CO aprox CN ^ ->} NO_2 ^ -> es> NH_3> underset { textrm {ligandos de campo intermedio}} { SCN ^ -> H_2O> oxalato ^ {2 -}}> OH ^ -> F> acetato ^ -> underset { textrm {ligandos de campo débil}} {Cl ^ -> Br ^ -> I ^ -}} )
Los valores de Δ o enumerados en la Tabla ( PageIndex {1} ) ilustran los efectos de la carga sobre el ion metálico, el número cuántico principal del metal y la naturaleza del ligando
Las mayores divisiones Δ o se encuentran en complejos de iones metálicos de la tercera fila de los metales de transición con cargas de al menos +3 y ligandos con pares de electrones solitarios localizados.
Colores de complejos de metales de transición
Los llamativos colores exhibidos por los complejos de metales de transición son causados por la excitación de un electrón de un orbital d de menor energía a un orbital d de mayor energía, que se llama transición d – d (Figura 24.6.3). Para que un fotón efectúe tal transición, su energía debe ser igual a la diferencia de energía entre los dos orbitales d, que depende de la magnitud de Δ o .
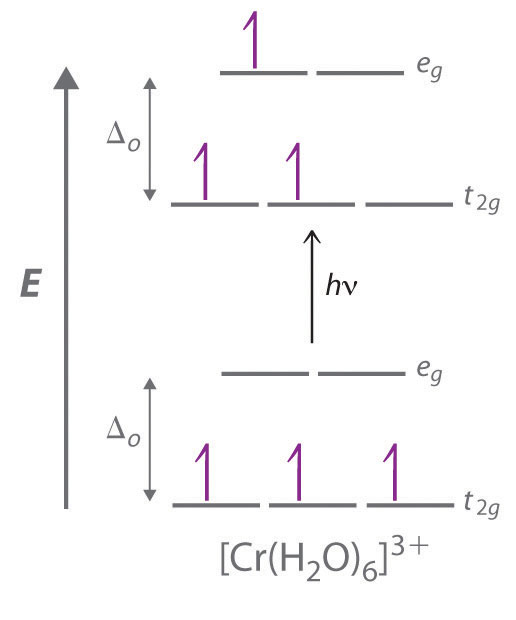
Recuerde que el color que observamos cuando miramos un objeto o un compuesto se debe a la luz que se transmite o refleja, no a la luz que se absorbe, y que la luz reflejada o transmitida es de color complementario a la luz que se absorbe . Por lo tanto, un compuesto verde absorbe luz en la porción roja del espectro visible y viceversa, como lo indica la rueda de color. Debido a que la energía de un fotón de luz es inversamente proporcional a su longitud de onda, el color de un complejo depende de la magnitud de Δ o , que depende de la estructura del complejo. Por ejemplo, el complejo [Cr (NH 3 ) 6 ] 3+ tiene ligandos de campo fuerte y un Δ o relativamente grande . En consecuencia, absorbe fotones de energía relativamente alta, correspondiente a la luz azul-violeta, que le da un color amarillo. Un complejo relacionado con ligandos de campo débil, el [Cr (H 2 O) 6 ] 3+ ion, absorbe los fotones de baja energía correspondientes al amarillo -parte verde del espectro visible, dándole un color violeta intenso.
Ahora podemos entender por qué las esmeraldas y los rubíes tienen colores tan diferentes, a pesar de que ambos contienen Cr 3 + en un entorno octaédrico proporcionado por seis iones de óxido. Aunque la identidad química de los seis ligandos es la misma en ambos casos, las distancias Cr-O son diferentes porque las composiciones de las redes del huésped son diferentes (Al 2 O 3 en rubíes y Be 3 Al 2 Si 6 O 18 en esmeraldas). En rubí, las distancias Cr-O son relativamente cortas debido a las restricciones de la red del huésped, lo que aumenta las interacciones d orbital-ligando y hace que Δ o sea relativamente grande. En consecuencia, los rubíes absorben la luz verde y la luz transmitida o reflejada es roja, lo que le da a la gema su color característico. En esmeralda, las distancias Cr-O son más largas debido a anillos de silicato relativamente grandes [Si 6 O 18 ] 12− ; esto da como resultado una disminución de las interacciones orbital-ligando d y un Δ más pequeño o . En consecuencia, las esmeraldas absorben la luz de una longitud de onda más larga (rojo), lo que le da a la gema su color verde característico. Está claro que el entorno del ion de metal de transición, que está determinado por la red del huésped, afecta dramáticamente las propiedades espectroscópicas de un ion metálico.

Energías de estabilización del campo de cristal
Recuerde que las moléculas estables contienen más electrones en los orbitales moleculares de menor energía (unión) en un diagrama de orbitales moleculares que en los orbitales moleculares de mayor energía (unión). Si el conjunto de orbitales d de energía más baja (los orbitales t 2g ) está poblado selectivamente por electrones, entonces la estabilidad del complejo aumenta. Por ejemplo, el único electrón d en el complejo ad 1 como [Ti (H 2 O) 6 ] 3+ se encuentra en uno de los orbitales t 2g . En consecuencia, este complejo será más estable de lo esperado en terrenos puramente electrostáticos en 0.4Δ o . La estabilización adicional de un complejo metálico por la población selectiva de los orbitales d de baja energía se denomina energía de estabilización de campo cristalino (CFSE). El CFSE de un complejo se puede calcular multiplicando el número de electrones en t 2g orbitales por la energía de esos orbitales (−0.4Δ o ), multiplicando el número de electrones en e g orbitales por la energía de esos orbitales (+ 0.6Δ o ), y sumando los dos. La tabla ( PageIndex {2} ) da valores CFSE para complejos octaédricos con diferentes configuraciones de electrones d. El CFSE es más alto para los complejos d 6 de baja rotación, lo que explica en parte la extraordinaria cantidad de complejos de Co (III) conocidos. Las otras configuraciones de bajo giro también tienen altos CFSEs, al igual que la configuración d 3 .
| High Spin | CFSE (Δ o ) | Giro bajo | CFSE (Δ o ) | |||
|---|---|---|---|---|---|---|
| d 0 | 0 | |||||
| d 1 | ↿ | 0,4 | ||||
| d 2 | ↿ ↿ | 0,8 | ||||
| d 3 | ↿ ↿ ↿ | 1.2 | ||||
| d 4 | ↿ ↿ ↿ | ↿ | 0,6 | ↿⇂ ↿ ↿ | 1,6 | |
| d 5 | ↿ ↿ ↿ | ↿ ↿ | 0,0 | ↿⇂ ↿⇂ ↿ | 2,0 | |
| d 6 | ↿⇂ ↿ ↿ | ↿ ↿ | 0,4 | ↿⇂ ↿⇂ ↿⇂ | 2,4 | |
| d 7 | ↿⇂ ↿⇂ ↿ | ↿ ↿ | 0,8 | ↿⇂ ↿⇂ ↿⇂ | ↿ | 1,8 |
| d 8 | ↿⇂ ↿⇂ ↿⇂ | ↿ ↿ | 1.2 | |||
| d 9 | ↿⇂ ↿⇂ ↿⇂ | ↿⇂ ↿ | 0,6 | |||
| d 10 | ↿⇂ ↿⇂ ↿⇂ | ↿⇂ ↿⇂ | 0.0 | |||
CFSEs are important for two reasons. First, the existence of CFSE nicely accounts for the difference between experimentally measured values for bond energies in metal complexes and values calculated based solely on electrostatic interactions. Second, CFSEs represent relatively large amounts of energy (up to several hundred kilojoules per mole), which has important chemical consequences.
Octahedral d 3 and d 8 complexes and low-spin d 6 , d 5 , d 7 , and d 4 complexes exhibit large CFSEs.
Summary
Crystal field theory, which assumes that metal–ligand interactions are only electrostatic in nature, explains many important properties of transition-metal complexes, including their colors, magnetism, structures, stability, and reactivity. Crystal field theory (CFT) is a bonding model that explains many properties of transition metals that cannot be explained using valence bond theory. In CFT, complex formation is assumed to be due to electrostatic interactions between a central metal ion and a set of negatively charged ligands or ligand dipoles arranged around the metal ion. Depending on the arrangement of the ligands, the d orbitals split into sets of orbitals with different energies. The difference between the energy levels in an octahedral complex is called the crystal field splitting energy (Δ o ), whose magnitude depends on the charge on the metal ion, the position of the metal in the periodic table, and the nature of the ligands. The spin-pairing energy (P) is the increase in energy that occurs when an electron is added to an already occupied orbital. A high-spin configuration occurs when the Δ o is less than P, which produces complexes with the maximum number of unpaired electrons possible. Conversely, a low-spin configuration occurs when the Δ o is greater than P, which produces complexes with the minimum number of unpaired electrons possible. Strong-field ligands interact strongly with the d orbitals of the metal ions and give a large Δ o , whereas weak-field ligands interact more weakly and give a smaller Δ o . The colors of transition-metal complexes depend on the environment of the metal ion and can be explained by CFT.