Vimos en el ejercicio del Ejemplo 6 en la Sección 15.2 que la constante de equilibrio para la descomposición de (CaCO_ {3 (s)} ) a (CaO _ {(s)} ) y (CO_ {2 (g)} ) es (K = [CO_2] ). A 800 ° C, la concentración de (CO_2 ) en equilibrio con el sólido (CaCO_3 ) y (CaO ) es (2.5 veces 10 ^ {- 3} ; M ). Por lo tanto, K a 800 ° C es (2.5 veces 10 ^ {- 3} ). (Recuerde que las constantes de equilibrio no tienen unidades).
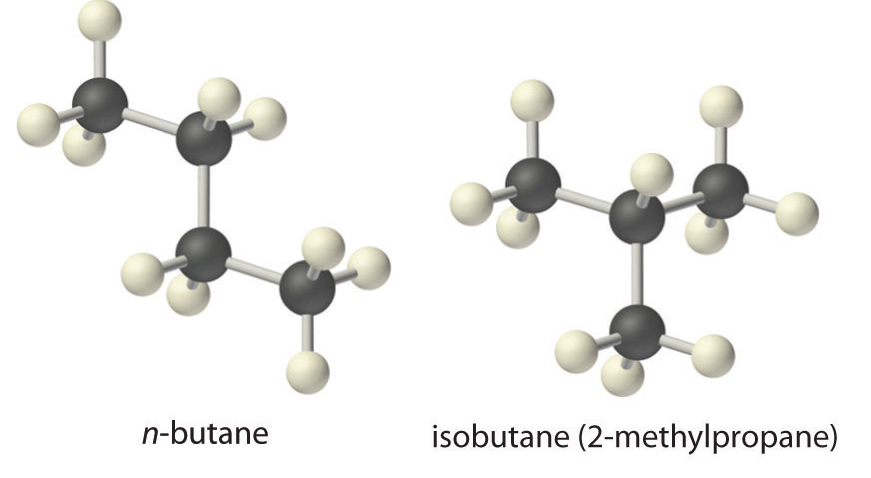
Un ejemplo más complejo de este tipo de problema es la conversión de n-butano, un aditivo utilizado para aumentar la volatilidad de la gasolina, en isobutano (2-metilpropano).
Esta reacción se puede escribir de la siguiente manera:
[ ce {n-butano _ {(g)} rightleftharpoons isobutane _ {(g)}} label {Eq1} ]
y la constante de equilibrio (K = [ text {isobutane}] / [ text {n-butane}] ). En equilibrio, se encontró que una mezcla de n-butano e isobutano a temperatura ambiente contenía 0,041 M de isobutano y 0,016 M de n-butano. Sustituyendo estas concentraciones en la expresión de equilibrio constante,
[K = dfrac {[ textit {isobutane}]} {[ textit {n-butane}]} = 0.041 ; M = 2.6 etiqueta {Eq2} ]
Por lo tanto, la constante de equilibrio para la reacción tal como está escrita es 2.6.
Ejemplo ( PageIndex {1} )
La reacción entre el dióxido de azufre gaseoso y el oxígeno es un paso clave en la síntesis industrial del ácido sulfúrico:
[2SO_ {2 (g)} + O_ {2 (g)} rightleftharpoons 2SO_ {3 (g)} nonumber ]
Una mezcla de (SO_2 ) y (O_2 ) se mantuvo a 800 K hasta que el sistema alcanzó el equilibrio. La mezcla de equilibrio contenía
(5.0 veces 10 ^ {- 2} ; M ; SO_3 ),
(3,5 veces 10 ^ {- 3} ; M ; O_2 ), y
(3.0 veces 10 ^ {- 3} ; M ; SO_2 ).
Calcule (K ) y (K_p ) a esta temperatura.
Dado : ecuación de equilibrio equilibrado y composición de la mezcla de equilibrio
Preguntado por : constante de equilibrio
Estrategia
Escribe la expresión de equilibrio constante para la reacción. Luego sustituya las concentraciones de equilibrio apropiadas en esta ecuación para obtener (K ).
SOLUCIÓN
Sustituyendo las concentraciones de equilibrio apropiadas en la expresión de equilibrio constante,
[K = dfrac {[SO_3] ^ 2} {[SO_2] ^ 2 [O_2]} = dfrac {(5.0 times 10 ^ {- 2}) ^ 2} {(3.0 times 10 ^ {- 3}) ^ 2 (3.5 times 10 ^ {- 3})} = 7.9 times 10 ^ 4 nonumber ]
Para resolver (K_p ), utilizamos la relación derivada previamente
[K_p = K (RT) ^ {Δn} ]
donde (Δn = 2 – 3 = −1 ):
[K_p = K (RT) ^ {Δn} nonumber ]
[K_p = 7.9 veces 10 ^ 4 [(0.08206 ; L⋅atm / mol⋅K) (800 K)] ^ {- 1} nonumber ]
[K_p = 1.2 times 10 ^ 3 nonumber ]
Ejercicio ( PageIndex {1} )
El gas hidrógeno y el yodo reaccionan para formar yoduro de hidrógeno a través de la reacción
[H_ {2 (g)} + I_ {2 (g)} rightleftharpoons 2HI _ {(g)} nonumber ]
Una mezcla de (H_2 ) y (I_2 ) se mantuvo a 740 K hasta que el sistema alcanzó el equilibrio. La mezcla de equilibrio contenía
(1.37 veces 10 ^ {- 2} ; M ; HI ),
(6,47 veces 10 ^ {- 3} ; M ; H_2 ), y
(5,94 por 10 ^ {- 4} ; M ; I_2 ).
Calcule (K ) y (K_p ) para esta reacción.
Respuesta
(K = 48.8 ) y (K_p = 48.8 )
Los químicos no suelen recibir las concentraciones de todas las sustancias, y no es probable que midan las concentraciones de equilibrio de todas las sustancias relevantes para un sistema en particular. En tales casos, podemos obtener las concentraciones de equilibrio de las concentraciones iniciales de los reactivos y la ecuación química equilibrada para la reacción, siempre que se conozca la concentración de equilibrio de una de las sustancias. El ejemplo ( PageIndex {2} ) muestra una forma de hacerlo.
Ejemplo ( PageIndex {2} )
Se colocó una muestra de 1,00 mol de (NOCl ) en un reactor de 2,00 L y se calentó a 227ºC hasta que el sistema alcanzó el equilibrio. Luego se analizaron los contenidos del reactor y se encontró que contenían 0,056 mol de (Cl_2 ). Calcule (K ) a esta temperatura. La ecuación para la descomposición de (NOCl ) a (NO ) y (Cl_2 ) es la siguiente:
[2 NOCl _ {(g)} rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} nonumber ]
Dado : ecuación de equilibrio equilibrado, cantidad de reactivo, volumen y cantidad de un producto en equilibrio
Preguntado por : (K )
Estrategia:
Escribe la expresión constante de equilibrio para la reacción. Construya una tabla que muestre las concentraciones iniciales, los cambios en las concentraciones y las concentraciones finales (como las concentraciones iniciales más los cambios en las concentraciones).
Calcule todas las concentraciones iniciales posibles a partir de los datos proporcionados e insértelos en la tabla.
Use los coeficientes en la ecuación química balanceada para obtener los cambios en la concentración de todas las otras sustancias en la reacción. Inserte esos cambios de concentración en la tabla.
Obtenga las concentraciones finales sumando las columnas. Calcule la constante de equilibrio para la reacción.
SOLUCIÓN
A El primer paso en cualquier problema de este tipo es equilibrar la ecuación química para la reacción (si aún no está equilibrada) y usarla para derivar la expresión constante de equilibrio. En este caso, la ecuación ya está equilibrada y la expresión constante de equilibrio es la siguiente:
[K = dfrac {[NO] ^ 2 [Cl_2]} {[NOCl] ^ 2} nonumber ]
Para obtener las concentraciones de (NOCl ), (NO ) y (Cl_2 ) en equilibrio, construimos una tabla que muestra lo que se sabe y lo que se debe calcular. Comenzamos escribiendo la ecuación química equilibrada en la parte superior de la tabla, seguida de tres líneas correspondientes a las concentraciones iniciales, los cambios en las concentraciones requeridas para pasar del estado inicial al final y las concentraciones finales.
[2 NOCl _ {(g)} rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} nonumber ]
ICE
([NOCl] )
([NO] )
([Cl_2] )
Inicial
Cambio
Final
B Inicialmente, el sistema contiene 1,00 mol de (NOCl ) en un recipiente de 2,00 l. Así ([NOCl] _i = 1.00 ; mol / 2.00 ; L = 0.500 ; M ). Las concentraciones iniciales de (NO ) y (Cl_2 ) son (0 ; M ) porque inicialmente no hay productos presentes. Además, se nos dice que en equilibrio el sistema contiene 0.056 mol de (Cl_2 ) en un contenedor de 2.00 L, entonces ([Cl_2] _f = 0.056 ; mol / 2.00 ; L = 0.028 ; M ). Insertamos estos valores en la siguiente tabla:
[2 NOCl _ {(g)} rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} nonumber ]
ICE
([NOCl] )
([NO] )
([Cl_2] )
Inicial
0,500
0
0
Cambio
Final
0,028
C Utilizamos las relaciones estequiométricas dadas en la ecuación química equilibrada para encontrar el cambio en la concentración de (Cl_2 ), la sustancia para la que se conocen las concentraciones iniciales y finales:
[Δ [Cl_2] = 0.028 ; M _ {(final)} – 0.00 ; M _ {(inicial)}] = +0.028 ; M nonumber ]
Según los coeficientes en la ecuación química equilibrada, se producen 2 mol de (NO ) por cada 1 mol de (Cl_2 ), por lo que el cambio en la concentración de (NO ) es el siguiente: [ 19459005]
[Δ [NO] = left ( dfrac {0.028 ; cancel {mol ; Cl_2}} {L} right) left ( dfrac {2 ; mol ; NO} {1 cancel {; mol ; Cl_2}} right) = 0.056 ; M nonumber ]
De manera similar, se consumen 2 mol de (NOCl ) por cada 1 mol de (Cl_2 ) producido, por lo que el cambio en la concentración de (NOCl ) es el siguiente:
[Δ [NOCl] = left ( dfrac {0.028 ; cancel {mol ; Cl_2}} {L} right) left ( dfrac {−2 ; mol ; NOCl} { 1 ; cancel {mol ; Cl_2}} right) = -0.056 ; M nonumber ]
Insertamos estos valores en nuestra tabla:
[2 NOCl _ {(g)} rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} nonumber ]
ICE
([NOCl] )
([NO] )
([Cl_2] )
Inicial
0,500
0
0
Cambio
−0,056
+0,056
+0,028
Final
0,028
D Sumamos los números en las columnas ([NOCl] ) y ([NO] ) para obtener las concentraciones finales de (NO ) y (NOCl ):
[[NO] _f = 0.000 ; M + 0.056 ; M = 0.056 ; M nonumber ]
[[NOCl] _f = 0.500 ; M + (−0.056 ; M) = 0.444 M nonumber ]
Ahora podemos completar la tabla:
[2 NOCl _ {(g)} rightleftharpoons 2NO _ {(g)} + Cl_ {2 (g)} nonumber ]
ICE
([NOCl]
([NO] )
([Cl_2] )
inicial
0,500
0
0
cambio
−0,056
+0,056
+0,028
final
0,444
0,056
0,028
Ahora podemos calcular la constante de equilibrio para la reacción:
[K = dfrac {[NO] ^ 2 [Cl_2]} {[NOCl] ^ 2} = dfrac {(0.056) ^ 2 (0.028)} {(0.444) ^ 2} = 4.5 veces 10 ^ {- 4} nonumber ]
Ejercicio ( PageIndex {2} )
El químico alemán Fritz Haber (1868–1934; Premio Nobel de Química 1918) pudo sintetizar amoníaco ( (NH_3 )) al reaccionar (0.1248 ; M ; H_2 ) y (0.0416 ; M ; N_2 ) a aproximadamente 500 ° C. En equilibrio, la mezcla contenía 0.00272 M (NH_3 ). ¿Qué es (K ) para la reacción
[N_2 + 3H_2 rightleftharpoons 2NH_3 nonumber ]
a esta temperatura? ¿Qué es (K_p )?
Respuesta
(K = 0.105 ) y (K_p = 2.61 times 10 ^ {- 5} )
Para describir cómo calcular las concentraciones de equilibrio a partir de una constante de equilibrio, primero consideramos un sistema que contiene un solo producto y un solo reactivo, la conversión de n-butano a isobutano (Ecuación ( ref {Eq1} ) ), para el cual K = 2.6 a 25 ° C. Si comenzamos con una muestra de n-butano de 1.00 M, podemos determinar la concentración de n-butano e isobutano en equilibrio construyendo una tabla que muestre lo que se sabe y lo que se debe calcular, tal como lo hicimos en el Ejemplo ( Índice de página {2} ).
[ text {n-butane} _ {(g)} rightleftharpoons text {isobutane} _ {(g)} ]
ICE
([ text {n-butano} _ {(g)}] )
([ text {isobutane} _ {(g)}] )
Inicial
Cambio
Final
Las concentraciones iniciales del reactivo y el producto son conocidas: [n-butano] i = 1.00 M e [isobutano] i = 0 M. Necesitamos calcular las concentraciones de equilibrio tanto de n-butano como de isobutano. Debido a que generalmente es difícil calcular las concentraciones finales directamente, nos enfocamos en el cambio en las concentraciones de las sustancias entre las condiciones inicial y final (equilibrio). Si, por ejemplo, definimos el cambio en la concentración de isobutano (Δ [isobutano]) como (+ x ), entonces el cambio en la concentración de n-butano es Δ [n-butano] = (- x ). Esto se debe a que la ecuación química equilibrada de la reacción nos dice que se consume 1 mol de n-butano por cada 1 mol de isobutano producido. Luego podemos expresar las concentraciones finales en términos de las concentraciones iniciales y los cambios que han sufrido.
[ text {n-butane} _ {(g)} rightleftharpoons text {isobutane} _ {(g)} ]
ICE
([ text {n-butano} _ {(g)}] )
([ text {isobutane} _ {(g)}] )
Inicial
1,00
0
Cambio
(- x )
(+ x )
Final
((1,00 – x) )
((0 + x) = x )
Sustituyendo las expresiones para las concentraciones finales de n-butano e isobutano de la tabla en la ecuación de equilibrio,
[K = dfrac {[ text {isobutane}]} {[ text {n-butane}]} = dfrac {x} {1.00 − x} = 2.6 ]
Reorganizando y resolviendo para (x ),
[x = 2.6 (1.00 − x) = 2.6−2.6x ]
[x + 2.6x = 2.6 ]
[x = 0,72 ]
Obtenemos las concentraciones finales sustituyendo este valor (x ) en las expresiones para las concentraciones finales de n-butano e isobutano que figuran en la tabla:
[[ text {n-butano}] _ f = (1.00 – x) M = (1.00 – 0.72) M = 0.28 ; M ]
[[ text {isobutane}] _ f = (0.00 + x) M = (0.00 + 0.72) M = 0.72 ; M ]
Podemos verificar los resultados sustituyéndolos nuevamente en la expresión constante de equilibrio para ver si dan la misma (K ) que usamos en el cálculo:
[K = dfrac {[ text {isobutane}]} {[ text {n-butane}]} = left ( dfrac {0.72 ; cancel {M}} {0.28 ; cancelar {M}} right) = 2.6 ]
Este es el mismo (K ) que nos dieron, por lo que podemos estar seguros de nuestros resultados.
El ejemplo ( PageIndex {3} ) ilustra un tipo común de problema de equilibrio que es probable que encuentre.
Ejemplo ( PageIndex {3} ): La reacción de cambio de agua y gas
La reacción de desplazamiento agua-gas es importante en varios procesos químicos, como la producción de H 2 para celdas de combustible. Esta reacción se puede escribir de la siguiente manera:
[H_ {2 (g)} + CO_ {2 (g)} rightleftharpoons H_2O _ {(g)} + CO _ {(g)} nonumber ]
(K = 0.106 ) a 700 K. Si una mezcla de gases que inicialmente contiene 0.0150 M (H_2 ) y 0.0150 M (CO_2 ) se equilibra a 700 K, ¿cuáles son las concentraciones finales? de todas las sustancias presentes?
Dado : ecuación de equilibrio equilibrado, (K ) y concentraciones iniciales
Preguntado: concentraciones finales
Estrategia :
Construya una tabla que muestre lo que se sabe y lo que debe calcularse. Defina (x ) como el cambio en la concentración de una sustancia. Luego use la estequiometría de reacción para expresar los cambios en las concentraciones de las otras sustancias en términos de (x ). A partir de los valores de la tabla, calcule las concentraciones finales.
Escribe la ecuación de equilibrio para la reacción. Sustituya los valores apropiados de la tabla ICE para obtener (x ).
Calcule las concentraciones finales de todas las especies presentes. Verifique sus respuestas sustituyendo estos valores en la expresión constante de equilibrio para obtener (K ).
SOLUCIÓN
A Las concentraciones iniciales de los reactivos son ([H_2] _i = [CO_2] _i = 0.0150 ; M ). Al igual que antes, nos centraremos en el cambio en las concentraciones de las diversas sustancias entre los estados inicial y final. Si definimos el cambio en la concentración de (H_2O ) como (x ), entonces (Δ [H_2O] = + x ). Podemos usar la estequiometría de la reacción para expresar los cambios en las concentraciones de las otras sustancias en términos de (x ). Por ejemplo, se produce 1 mol de (CO ) por cada 1 mol de (H_2O ), por lo que el cambio en la concentración de (CO ) se puede expresar como (Δ [CO] = + x ) . Del mismo modo, por cada 1 mol de (H_2O ) producido, se consume 1 mol de (H_2 ) y (CO_2 ), por lo que el cambio en la concentración de los reactivos es (Δ [H_2] = Δ [CO_2] = −x ). Ingresamos los valores en la siguiente tabla y calculamos las concentraciones finales.
[H_ {2 (g)} + CO_ {2 (g)} rightleftharpoons H_2O _ {(g)} + CO _ {(g)} nonumber ]
ICE
([H_2] )
([CO_2] )
([H_2O] )
([CO] )
Inicial
0,0150
0,0150
0
0
Cambio
(- x )
(- x )
(+ x )
(+ x )
Final
((0,0150 – x) )
((0,0150 – x) )
(x )
(x )
B Ahora podemos usar la ecuación de equilibrio y la (K ) dada para resolver (x ):
[K = dfrac {[H_2O] [CO]} {[H_2] [CO_2]} = dfrac {(x) (x)} {(0.0150 − x) (0.0150 − x} = dfrac {x ^ 2} {(0.0150 − x) ^ 2} = 0.106 nonumber ]
Podríamos resolver esta ecuación con la fórmula cuadrática, pero es mucho más fácil resolver (x ) al reconocer que el lado izquierdo de la ecuación es un cuadrado perfecto; es decir,
[ dfrac {x ^ 2} {(0.0150 − x) ^ 2} = left ( dfrac {x} {0.0150 − x} right) ^ 2 = 0.106 nonumber ]
Tomando la raíz cuadrada de los términos medio y derecho,
[ dfrac {x} {(0.0150 − x)} = (0.106) ^ {1/2} = 0.326 nonumber ]
[x = (0.326) (0.0150) −0.326x nonumber ]
[1.326x = 0.00489 nonumber ]
[x = 0.00369 = 3.69 veces 10 ^ {- 3} nonumber ]
C Las concentraciones finales de todas las especies en la mezcla de reacción son las siguientes:
([H_2] _f = [H_2] _i + Δ [H_2] = (0.0150−0.00369) ; M = 0.0113 ; M )
([CO_2] _f = [CO_2] _i + Δ [CO_2] = (0.0150−0.00369) ; M = 0.0113 ; M )
([H_2O] _f = [H_2O] _i + Δ [H_2O] = (0 + 0.00369) ; M = 0.00369 ; M )
([CO] _f = [CO] _i + Δ [CO] = (0 + 0.00369) ; M = 0.00369 ; M )
Podemos verificar nuestro trabajo insertando los valores calculados nuevamente en la expresión constante de equilibrio:
[K = dfrac {[H_2O] [CO]} {[H_2] [CO_2]} = dfrac {(0.00369) ^ 2} {(0.0113) ^ 2} = 0.107 nonumber ] [19459005 ]
Para dos cifras significativas, esta K es igual al valor dado en el problema, por lo que nuestra respuesta está confirmada.
Ejercicio ( PageIndex {3} )
El gas hidrógeno reacciona con el vapor de yodo para dar yoduro de hidrógeno de acuerdo con la siguiente ecuación química:
[H_ {2 (g)} + I_ {2 (g)} rightleftharpoons 2HI _ {(g)} nonumber ]
(K = 54 ) a 425 ° C. Si se inyectan 0.172 M (H_2 ) y (I_2 ) en un reactor y se mantienen a 425 ° C hasta que el sistema se equilibre, ¿cuál es la concentración final de cada sustancia en la mezcla de reacción?
Respuesta
([HI] _f = 0.270 ; M )
([H_2] _f = [I_2] _f = 0.037 ; M )
En el Ejemplo ( PageIndex {3} ), las concentraciones iniciales de los reactivos fueron las mismas, lo que nos dio una ecuación que era un cuadrado perfecto y simplificó nuestros cálculos. Sin embargo, a menudo, las concentraciones iniciales de los reactivos no son las mismas, y / o uno o más de los productos pueden estar presentes cuando comienza la reacción. En estas condiciones, generalmente no hay forma de simplificar el problema, y debemos determinar las concentraciones de equilibrio con otros medios. Tal caso se describe en el Ejemplo ( PageIndex {4} ).
Ejemplo ( PageIndex {4} )
En la reacción de cambio de agua y gas que se muestra en el Ejemplo ( PageIndex {3} ), una muestra que contiene 0.632 M CO2 y 0.570 M (H_2 ) se equilibra a 700 K. A esta temperatura, (K = 0,106 ). ¿Cuál es la composición de la mezcla de reacción en equilibrio?
Dado : ecuación de equilibrio equilibrado, concentraciones de reactivos y (K )
Preguntado por : composición de la mezcla de reacción en equilibrio
Estrategia :
Escribe la ecuación de equilibrio. Construya una tabla que muestre las concentraciones iniciales de todas las sustancias en la mezcla. Complete la tabla que muestra los cambios en las concentraciones ( (x) y las concentraciones finales.
Escribe la expresión constante de equilibrio para la reacción. Sustituya el valor K conocido y las concentraciones finales para resolver (x ).
Calcule la concentración final de cada sustancia en la mezcla de reacción. Verifique sus respuestas sustituyendo estos valores en la expresión constante de equilibrio para obtener (K ).
SOLUCIÓN
A ([CO_2] _i = 0.632 ; M ) y ([H_2] _i = 0.570 ; M ). Nuevamente, (x ) se define como el cambio en la concentración de (H_2O ): (Δ [H_2O] = + x ). Debido a que se produce 1 mol de (CO ) por cada 1 mol de (H_2O ), el cambio en la concentración de (CO ) es el mismo que el cambio en la concentración de H2O, entonces Δ [CO] = + x. De manera similar, debido a que se consume 1 mol de (H_2 ) y (CO_2 ) por cada 1 mol de (H_2O ) producido, (Δ [H_2] = Δ [CO_2] = −x ). Las concentraciones finales son las sumas de las concentraciones iniciales y los cambios en las concentraciones en equilibrio.
[H_ {2 (g)} + CO_ {2 (g)} rightleftharpoons H_2O _ {(g)} + CO _ {(g)} nonumber ]
ICE
(H_ {2 (g)} )
(CO_ {2 (g)} )
(H_2O _ {(g)} )
(CO _ {(g)} )
Inicial
0,570
0,632
0
0
Cambio
(- x )
(- x )
(+ x )
(+ x )
Final
((0,570 – x) )
((0,632 – x) )
(x )
(x )
B Ahora podemos usar la ecuación de equilibrio y el valor conocido de (K ) para resolver (x ):
[K = dfrac {[H_2O] [CO]} {[H_2] [CO_2]} = dfrac {x ^ 2} {(0.570 − x) (0.632 − x)} = 0.106 nonumber ]
En contraste con el Ejemplo ( PageIndex {3} ), sin embargo, no hay una manera obvia de simplificar esta expresión. Por lo tanto, debemos expandir la expresión y multiplicar ambos lados por el denominador:
[x ^ 2 = 0.106 (0.360 – 1.202x + x ^ 2) nonumber ]
Recolección de términos en un lado de la ecuación,
[0.894x ^ 2 + 0.127x – 0.0382 = 0 nonumber ]
Esta ecuación se puede resolver usando la fórmula cuadrática:
[x = dfrac {-b pm sqrt {b ^ 2-4ac}} {2a} = dfrac {−0.127 pm sqrt {(0.127) ^ 2−4 (0.894) (- 0.0382)}} {2 (0.894)} nonumber ]
[x = 0.148 text {y} −0.290 nonumber ]
Solo la respuesta con el valor positivo tiene algún significado físico, entonces (Δ [H_2O] = Δ [CO] = +0.148 M ), y (Δ [H_2] = Δ [CO_2] = −0.148 ; M ).
C Las concentraciones finales de todas las especies en la mezcla de reacción son las siguientes:
([H_2] _f [= [H_2] _i + Δ [H_2] = 0.570 ; M −0.148 ; M = 0.422 M )
([CO_2] _f = [CO_2] _i + Δ [CO_2] = 0.632 ; M − 0.148 ; M = 0.484 M )
([H_2O] _f = [H_2O] _i + Δ [H_2O] = 0 ; M + 0.148 ; M = 0.148 ; M )
([CO] _f = [CO] _i + Δ [CO] = 0 M + 0.148 ; M = 0.148 M )
Podemos verificar nuestro trabajo sustituyendo estos valores en la expresión de equilibrio constante:
[K = dfrac {[H_2O] [CO]} {[H_2] [CO_2]} = dfrac {(0.148) ^ 2} {(0.422) (0.484)} = 0.107 nonumber ] [ 19459005]
Debido a que (K ) es esencialmente el mismo que el valor dado en el problema, nuestros cálculos están confirmados.
Ejercicio ( PageIndex {4} )
El ejercicio del Ejemplo ( PageIndex {1} ) mostró la reacción del hidrógeno y el vapor de yodo para formar yoduro de hidrógeno, para el cual (K = 54 ) a 425 ° C. Si una muestra que contiene 0.200 M (H_2 ) y 0.0450 M (I_2 ) se equilibra a 425 ° C, ¿cuál es la concentración final de cada sustancia en la mezcla de reacción?
Respuesta
([H_I] _f = 0.0882 ; M )
([H_2] _f = 0.156 ; M )
([I_2] _f = 9.2 veces 10 ^ {- 4} M )
En muchas situaciones no es necesario resolver una ecuación cuadrática (o de orden superior). La mayoría de estos casos implican reacciones para las cuales la constante de equilibrio es muy pequeña ( (K ≤ 10 ^ {- 3} )) o muy grande ( (K ≥ 10 ^ 3 )), lo que significa que el cambio en la concentración (definida como (x )) es esencialmente insignificante en comparación con la concentración inicial de una sustancia. Saber esto simplifica los cálculos dramáticamente, como se ilustra en el Ejemplo ( PageIndex {5} ).
Ejemplo ( PageIndex {5} )
El nitrógeno atmosférico y el oxígeno reaccionan para formar óxido nítrico:
[N_ {2 (g)} + O_ {2 (g)} rightleftharpoons 2NO _ {(g)} nonumber ]
con (K_p = 2.0 times 10 ^ {- 31} ) a 25 ° C.
¿Cuál es la presión parcial de NO en equilibrio con (N_2 ) y (O_2 ) en la atmósfera (a 1 atm, (P_ {N_2} = 0.78 ; atm ) y (P_ { O_2} = 0.21 ; atm )?
Dado : ecuación de equilibrio equilibrado y valores de (K_p ), (P_ {O_2} ) y (P_ {N_2} )
Preguntado por : presión parcial de NO
Estrategia :
Construya una tabla e ingrese las presiones parciales iniciales, los cambios en las presiones parciales que ocurren durante el curso de la reacción y las presiones parciales finales de todas las sustancias.
Escribe la ecuación de equilibrio para la reacción. Luego, sustituya los valores de la tabla para resolver el cambio de concentración ( (x).
Calcule la presión parcial de (NO ). Verifique su respuesta sustituyendo valores en la ecuación de equilibrio y resolviendo (K ).
SOLUCIÓN
A Debido a que se nos da Kp y se informan presiones parciales en atmósferas, utilizaremos presiones parciales. La presión parcial inicial de (O_2 ) es 0.21 atm y la de (N_2 ) es 0.78 atm. Si definimos el cambio en la presión parcial de (NO ) como (2x ), entonces el cambio en la presión parcial de (O_2 ) y de (N_2 ) es (- x ) porque Se consume 1 mol de (N_2 ) y de (O_2 ) por cada 2 mol de NO producido. Cada sustancia tiene una presión parcial final igual a la suma de la presión inicial y el cambio en esa presión en el equilibrio.
[N_ {2 (g)} + O_ {2 (g)} rightleftharpoons 2NO _ {(g)} nonumber ]
ICE
(P_ {N_2} )
(P_ {O_2} )
(P_ {NO} )
Inicial
0,78
0,21
0
Cambio
(- x )
(- x )
(+ 2x )
Final
((0.78 − x))
((0.21 − x))
(2x)
B Substituting these values into the equation for the equilibrium constant,
[K_p=dfrac{(P_{NO})^2}{(P_{N_2})(P_{O_2})}=dfrac{(2x)^2}{(0.78−x)(0.21−x)}=2.0 times 10^{−31}nonumber]
In principle, we could multiply out the terms in the denominator, rearrange, and solve the resulting quadratic equation. In practice, it is far easier to recognize that an equilibrium constant of this magnitude means that the extent of the reaction will be very small; therefore, the (x) value will be negligible compared with the initial concentrations. If this assumption is correct, then to two significant figures, ((0.78 − x) = 0.78) and ((0.21 − x) = 0.21). Substituting these expressions into our original equation,
[dfrac{(2x)^2}{(0.78)(0.21)} = 2.0 times 10^{−31nonumber}]
[dfrac{4x^2}{0.16} =2.0 times10^{−31}nonumber]
[x^2=dfrac{0.33 times 10^{−31}}{4}nonumber]
[x^=9.1 times 10^{−17}nonumber]
C Substituting this value of (x) into our expressions for the final partial pressures of the substances,
(P_{NO}=2x ; atm=1.8 times 10^{−16} ;atm )
(P_{N_2}=(0.78−x) ;atm=0.78 ;atm )
(P_{O_2}=(0.21−x) ;atm=0.21; atm)
From these calculations, we see that our initial assumption regarding (x) was correct: given two significant figures, (2.0 times 10^{−16}) is certainly negligible compared with 0.78 and 0.21. When can we make such an assumption? As a general rule, if (x) is less than about 5% of the total, or (10^{−3} > K > 10^3), then the assumption is justified. Otherwise, we must use the quadratic formula or some other approach. The results we have obtained agree with the general observation that toxic (NO), an ingredient of smog, does not form from atmospheric concentrations of (N_2) and (O_2) to a substantial degree at 25°C. We can verify our results by substituting them into the original equilibrium equation:
[K_p=dfrac{(P_{NO})^2}{(P_{N_2})(P_{O_2})}=dfrac{(1.8 times 10^{−16})^2}{(0.78)(0.21)}=2.0 times 10^{−31}nonumber]
The final (K_p) agrees with the value given at the beginning of this example.
Exercise (PageIndex{5})
Under certain conditions, oxygen will react to form ozone, as shown in the following equation:
[3O_{2(g)} rightleftharpoons 2O_{3(g)}nonumber]
with (K_p = 2.5 times 10^{−59}) at 25°C. What ozone partial pressure is in equilibrium with oxygen in the atmosphere ((P_{O_2}=0.21; atm))?
Answer
(4.8 times 10^{−31} ;atm)
Another type of problem that can be simplified by assuming that changes in concentration are negligible is one in which the equilibrium constant is very large ((K geq 10^3)). A large equilibrium constant implies that the reactants are converted almost entirely to products, so we can assume that the reaction proceeds 100% to completion. When we solve this type of problem, we view the system as equilibrating from the products side of the reaction rather than the reactants side. This approach is illustrated in Example (PageIndex{6}).
Example (PageIndex{6})
The chemical equation for the reaction of hydrogen with ethylene ((C_2H_4)) to give ethane ((C_2H_6)) is as follows:
[H_{2(g)}+C_2H_{4(g)} overset{Ni}{rightleftharpoons} C_2H_{6(g)}nonumber]
with (K = 9.6 times 10^{18}) at 25°C. If a mixture of 0.200 M (H_2) and 0.155 M (C_2H_4) is maintained at 25°C in the presence of a powdered nickel catalyst, what is the equilibrium concentration of each substance in the mixture?
Given : balanced chemical equation, (K), and initial concentrations of reactants
Asked for : equilibrium concentrations
Strategy :
Construct a table showing initial concentrations, concentrations that would be present if the reaction were to go to completion, changes in concentrations, and final concentrations.
Write the equilibrium constant expression for the reaction. Then substitute values from the table into the expression to solve for (x) (the change in concentration).
Calculate the equilibrium concentrations. Check your answers by substituting these values into the equilibrium equation.
Solution :
A From the magnitude of the equilibrium constant, we see that the reaction goes essentially to completion. Because the initial concentration of ethylene (0.155 M) is less than the concentration of hydrogen (0.200 M), ethylene is the limiting reactant; that is, no more than 0.155 M ethane can be formed from 0.155 M ethylene. If the reaction were to go to completion, the concentration of ethane would be 0.155 M and the concentration of ethylene would be 0 M. Because the concentration of hydrogen is greater than what is needed for complete reaction, the concentration of unreacted hydrogen in the reaction mixture would be 0.200 M − 0.155 M = 0.045 M. The equilibrium constant for the forward reaction is very large, so the equilibrium constant for the reverse reaction must be very small. The problem then is identical to that in Example (PageIndex{5}). If we define (−x) as the change in the ethane concentration for the reverse reaction, then the change in the ethylene and hydrogen concentrations is (+x). The final equilibrium concentrations are the sums of the concentrations for the forward and reverse reactions.
[H_{2(g)}+C_2H_{4(g)} overset{Ni}{rightleftharpoons} C_2H_{6(g)}nonumber]
IACE
([H_{2(g)}])
([C_2H_{4(g)}])
([C_2H_{6(g)}])
Initial
0.200
0.155
0
Assuming 100% reaction
0.045
0
0.155
Change
(+x)
(+x)
(−x)
Final
((0.045 + x))
((0 + x))
((0.155 − x))
B Substituting values into the equilibrium constant expression,
[K=dfrac{[C_2H_6]}{[H_2][C_2H_4]}=dfrac{0.155−x}{(0.045+x)x}=9.6 times 10^{18}nonumber]
Once again, the magnitude of the equilibrium constant tells us that the equilibrium will lie far to the right as written, so the reverse reaction is negligible. Thus (x) is likely to be very small compared with either 0.155 M or 0.045 M, and the equation can be simplified (((0.045 + x)) = 0.045 and ((0.155 − x) = 0.155)) as follows:
[K=dfrac{0.155}{0.045x} = 9.6 times 10^{18}nonumber]
[x=3.6 times 10^{−19}nonumber]
C The small (x) value indicates that our assumption concerning the reverse reaction is correct, and we can therefore calculate the final concentrations by evaluating the expressions from the last line of the table:
([C_2H_6]_f = (0.155 − x); M = 0.155 ; M)
([C_2H_4]_f = x; M = 3.6 times 10^{−19} M )
([H_2]_f = (0.045 + x) ;M = 0.045 ;M)
We can verify our calculations by substituting the final concentrations into the equilibrium constant expression:
[K=dfrac{[C_2H_6]}{[H_2][C_2H_4]}=dfrac{0.155}{(0.045)(3.6 times 10^{−19})}=9.6 times 10^{18}nonumber]
This (K) value agrees with our initial value at the beginning of the example.
Exercise (PageIndex{6})
Hydrogen reacts with chlorine gas to form hydrogen chloride:
[H_{2(g)}+Cl_{2(g)} rightleftharpoons 2HCl_{(g)}nonumber]
with (K_p = 4.0 times 10^{31}) at 47°C. If a mixture of 0.257 M (H_2) and 0.392 M (Cl_2) is allowed to equilibrate at 47°C, what is the equilibrium composition of the mixture?
Answer
([H_2]_f = 4.8 times 10^{−32}; M) ([Cl_2]_f = 0.135; M) ([HCl]_f = 0.514; M)