Directrices para el análisis de circuitos combinados serie-paralelo
El objetivo del análisis del circuito de resistencia en serie-paralelo es poder determinar todas las caídas de voltaje, corrientes y disipaciones de potencia en un circuito. La estrategia general para lograr este objetivo es la siguiente:
- Paso 1: Evalúe qué resistencias en un circuito están conectadas entre sí en series simples o en paralelo simple.
- Paso 2: Vuelva a dibujar el circuito, reemplazando cada una de esas combinaciones de resistencias en serie o en paralelo identificadas en el paso 1 con una sola resistencia de valor equivalente. Si usa una tabla para administrar variables, cree una nueva columna de tabla para cada resistencia equivalente.
- Paso 3: Repita los pasos 1 y 2 hasta que todo el circuito se reduzca a una resistencia equivalente.
- Paso 4: Calcule la corriente total a partir del voltaje total y la resistencia total (I = E / R).
- Paso 5: Tomando los valores de voltaje total y corriente total, regrese al último paso en el proceso de reducción de circuito e inserte esos valores donde corresponda.
- Paso 6: De las resistencias conocidas y los valores de voltaje total / corriente total del paso 5, use la Ley de Ohm para calcular valores desconocidos (voltaje o corriente) (E = IR o I = E / R).
- Paso 7: Repita los pasos 5 y 6 hasta que todos los valores de voltaje y corriente se conozcan en la configuración original del circuito. Esencialmente, procederá paso a paso desde la versión simplificada del circuito a su forma original y compleja, conectando los valores de voltaje y corriente donde sea apropiado hasta que se conozcan todos los valores de voltaje y corriente.
- Paso 8: Calcule las disipaciones de potencia de los valores conocidos de voltaje, corriente y / o resistencia .
Ejemplo de análisis de circuito combinado serie-paralelo
Esto puede sonar como un proceso intimidante, pero es mucho más fácil de entender a través del ejemplo que a través de la descripción.
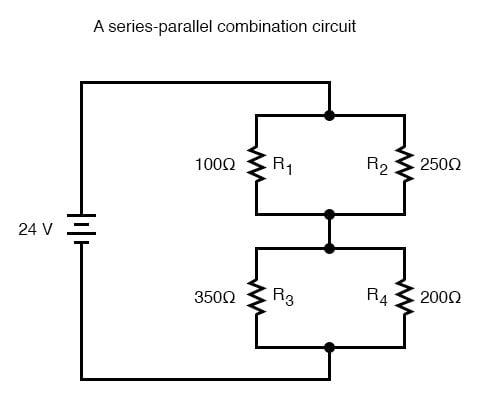

Cálculo de resistencias paralelas
En el circuito de ejemplo anterior, R 1 y R 2 están conectados en una disposición paralela simple, al igual que R 3 y R 4 . Una vez identificadas, estas secciones deben convertirse en resistencias individuales equivalentes , y el circuito se vuelve a dibujar:

Los símbolos de doble barra (//) representan “paralelo” para mostrar que los valores de resistencia equivalentes se calcularon utilizando la fórmula 1 / (1 / R). La resistencia de 71.429 Ω en la parte superior del circuito es el equivalente de R 1 y R 2 en paralelo entre sí. La resistencia de 127.27 Ω en la parte inferior es el equivalente de R 3 y R 4 en paralelo entre sí.
Nuestra tabla se puede ampliar para incluir estos equivalentes de resistencia en sus propias columnas:

Ahora debería ser evidente que el circuito se ha reducido a una configuración en serie simple con solo dos resistencias (equivalentes). El paso final en la reducción es agregar estas dos resistencias para obtener una resistencia total del circuito. Cuando sumamos esas dos resistencias equivalentes, obtenemos una resistencia de 198.70 Ω. Ahora, podemos volver a dibujar el circuito como una resistencia equivalente única y agregar la cifra de resistencia total a la columna más a la derecha de nuestra tabla. Tenga en cuenta que la columna “Total” se ha vuelto a etiquetar (R 1 // R 2 —R 3 // R 4 ) a Indique cómo se relaciona eléctricamente con las otras columnas de figuras. El símbolo “-” se usa aquí para representar “series”, así como el símbolo “//” se usa para representar “paralelo”.
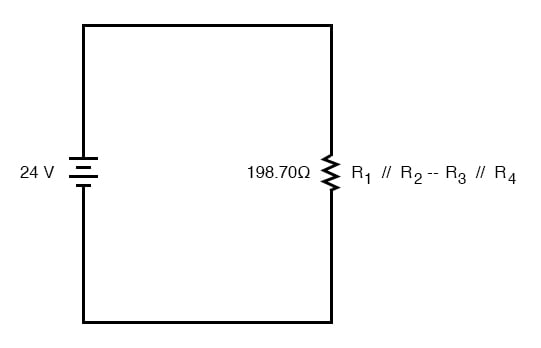

Cálculo de corriente y voltajes
Ahora, la corriente total del circuito se puede determinar aplicando Ley de Ohm (I = E / R) a la columna “Total” en la tabla:

Volviendo a nuestro dibujo de circuito equivalente, nuestro valor de corriente total de 120,78 miliamperios se muestra como la única corriente aquí:

Ahora comenzamos a trabajar hacia atrás en nuestra progresión de rediseños de circuitos a la configuración original. El siguiente paso es ir al circuito donde R 1 // R 2 y R 3 // R 4 están en serie :
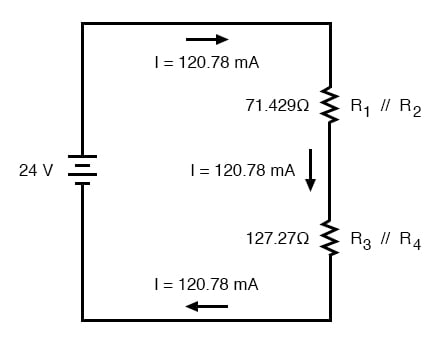
Dado que R 1 // R 2 y R 3 // R 4 están en serie entre sí, la corriente a través de esos dos conjuntos de resistencias equivalentes deben ser iguales. Además, la corriente a través de ellos debe ser la misma que la corriente total, por lo que podemos completar nuestra tabla con los valores actuales apropiados, simplemente copiando la cifra actual de la columna Total a R 1 // R 2 y R 3 // R 4 columnas:

Ahora, conociendo la corriente a través de las resistencias equivalentes R 1 // R 2 y R 3 // R 4 , podemos aplicar la Ley de Ohm (E = IR) a las dos columnas verticales derechas para encontrar caídas de voltaje en ellas:


Porque sabemos que R 1 // R 2 y R 3 // R 4 son equivalentes de resistencia paralelos, y nosotros Sabemos que las caídas de voltaje en circuitos paralelos son las mismas, podemos transferir las caídas de voltaje respectivas a las columnas apropiadas en la tabla para esas resistencias individuales. En otras palabras, damos otro paso atrás en nuestra secuencia de dibujo a la configuración original, y completamos la tabla en consecuencia:


Finalmente, la sección original de la tabla (columnas R 1 a R 4 ) está completa con suficientes valores para terminar. Aplicando la Ley de Ohm a las columnas verticales restantes (I = E / R), podemos determinar las corrientes a través de R 1 , R 2 , R 3 , y R 4 individualmente:

Colocación de valores de voltaje y corriente en diagramas
Habiendo encontrado todos los valores de voltaje y corriente para este circuito, podemos mostrar esos valores en el diagrama esquemático como tal:
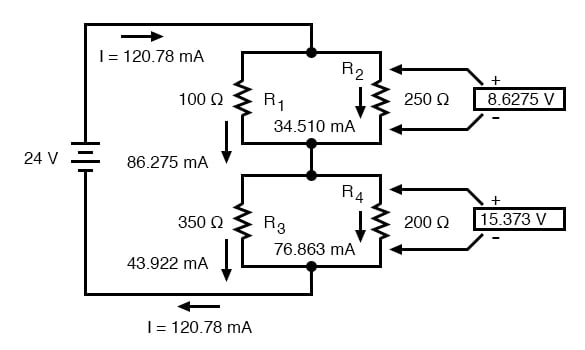
Como verificación final de nuestro trabajo, podemos ver si los valores actuales calculados se suman como deberían al total. Dado que R 1 y R 2 están en paralelo, sus corrientes combinadas deberían sumar el total de 120,78 mA. Del mismo modo, dado que R 3 y R 4 están en paralelo, sus corrientes combinadas también deberían sumar el total de 120,78 mA. Puede verificarlo usted mismo para verificar que estas cifras se sumen como se esperaba.
Uso de SPICE para verificar valores calculados
Una simulación por computadora también se puede utilizar para verificar la precisión de estas cifras. El siguiente análisis SPICE mostrará todos los voltajes y corrientes de resistencia (tenga en cuenta las fuentes de voltaje “simuladas” vi1, vi2, … con detección de corriente en serie con cada resistencia en la lista de redes, necesarias para que el programa informático SPICE rastree la corriente a través de cada ruta ) Estas fuentes de voltaje se configurarán para tener valores de cero voltios cada una para que no afecten el circuito de ninguna manera.

circuito en serie-paralelo v1 1 0 vi1 1 2 dc 0 vi2 1 3 dc 0 r1 2 4 100 r2 3 4 250 vi3 4 5 dc 0 vi4 4 6 dc 0 r3 5 0 350 r4 6 0 200 .dc v1 24 24 1 .print dc v (2,4) v (3,4) v (5,0) v (6,0) .print dc i (vi1) i (vi2) i (vi3) i (vi4) .final
He anotado las cifras de salida de SPICE para hacerlas más legibles, indicando qué cifras de voltaje y corriente pertenecen a qué resistencias.
| v1 | v (2,4) | v (3,4) | v (5) | v (6) |
|---|---|---|---|---|
| 2,40E + 01 | 8.63E + 00 | 8.63E + 00 | 1.54E + 01 | 1.54E + 01 |
| Voltaje de la batería | Tensión R1 | Voltaje R2 | Tensión R3 | Tensión R4 |
| v1 | i (vi1) | i (vi2) | i (vi3) | i (vi4) |
|---|---|---|---|---|
| 2,40E + 01 | 8.63E-02 | 3.54EE-02 | 4.39E-02 | 7.69E-02 |
| Voltaje de la batería | Corriente R1 | Corriente R2 | Corriente R3 | Corriente R4 |
Como puede ver, todas las cifras coinciden con los valores calculados.
REVISIÓN:
- Para analizar un circuito combinado serie-paralelo, siga estos pasos:
- Reduzca el circuito original a una resistencia equivalente única, volviendo a dibujar el circuito en cada paso de reducción a medida que las series simples y las partes paralelas simples se reducen a resistencias equivalentes individuales.
- Resolver para resistencia total.
- Resolver para corriente total (I = E / R).
- Determine las caídas de voltaje de la resistencia equivalente y las corrientes de derivación una etapa a la vez, trabajando hacia atrás a la configuración original del circuito nuevamente.
HOJAS DE TRABAJO RELACIONADAS: