¿Qué es la Ley de Voltaje de Kirchhoff (KVL)?
El principio conocido como Ley de voltaje de Kirchhoff (descubierto en 1847 por Gustav R. Kirchhoff, un físico alemán) puede establecerse como tal:
“La suma algebraica de todos los voltajes en un bucle debe ser igual a cero”
Por algebraico , me refiero a tener en cuenta los signos (polaridades) y las magnitudes. Con loop , me refiero a cualquier camino trazado desde un punto en un circuito alrededor de otros puntos en ese circuito, y finalmente de vuelta al punto inicial.
Demostrando la ley de voltaje de Kirchhoff en un circuito en serie
Veamos nuevamente nuestro circuito en serie de ejemplo, esta vez numerando los puntos en el circuito para referencia de voltaje:

Si tuviéramos que conectar un voltímetro entre los puntos 2 y 1, el cable de prueba rojo al punto 2 y el cable de prueba negro al punto 1, el medidor registraría +45 voltios. Normalmente, el signo “+” no se muestra, sino que está implícito, para lecturas positivas en pantallas de medidores digitales. Sin embargo, para esta lección, la polaridad de la lectura de voltaje es muy importante, por lo que mostraré números positivos explícitamente:

Cuando se especifica un voltaje con un subíndice doble (los caracteres “2-1” en la notación “E 2-1 ”), significa el voltaje en el primer punto (2) medido en referencia al segundo punto (1). Un voltaje especificado como “E cd ” significaría el voltaje indicado por un medidor digital con el cable de prueba rojo en el punto “c” y el cable de prueba negro en el punto “d”: el voltaje en “c “En referencia a” d “.

Si tuviéramos que tomar el mismo voltímetro y medir la caída de voltaje en cada resistencia , dando la vuelta al circuito en sentido horario con el cable rojo de prueba de nuestro medidor en el punto por delante y la prueba negra en el punto de atrás, obtendríamos las siguientes lecturas:


Ya deberíamos estar familiarizados con el principio general de los circuitos en serie que indica que las caídas de voltaje individuales se suman al voltaje total aplicado, pero medir el voltaje cae de esta manera y prestar atención a la polaridad (signo matemático ) de las lecturas revela otra faceta de este principio: que todos los voltajes medidos como tales suman cero:

En el ejemplo anterior, el bucle se formó mediante los siguientes puntos en este orden: 1-2-3-4-1. No importa en qué punto comencemos o en qué dirección procedamos al rastrear el ciclo; la suma de voltaje seguirá siendo igual a cero. Para demostrarlo, podemos sumar los voltajes en el bucle 3-2-1-4-3 del mismo circuito:

Esto puede tener más sentido si volvemos a dibujar nuestro circuito en serie de ejemplo para que todos los componentes estén representados en línea recta:

Sigue siendo el mismo circuito en serie, solo que con los componentes dispuestos en una forma diferente. Observe las polaridades de las caídas de voltaje de la resistencia con respecto a la batería: el voltaje de la batería es negativo a la izquierda y positivo a la derecha, mientras que todas las caídas de voltaje de la resistencia están orientadas hacia el otro lado: positivo a la izquierda y negativo a la derecha. Esto se debe a que las resistencias resisten al flujo de carga eléctrica que empuja la batería. En otras palabras, el “empuje” ejercido por las resistencias contra el flujo de carga eléctrica debe estar en una dirección opuesta a la fuente de fuerza electromotriz.
Aquí vemos lo que un voltímetro digital indicaría a través de cada componente en este circuito, el cable negro a la izquierda y el cable rojo a la derecha, tal como se presenta en forma horizontal:

Si tuviéramos que tomar el mismo voltímetro y leer el voltaje a través de combinaciones de componentes, comenzando con el único R 1 a la izquierda y progresando en toda la cadena de componentes, veremos cómo se suman los voltajes algebraicamente (a cero):

El hecho de que se sumen voltajes en serie no debería ser un misterio, pero notamos que la polaridad de estos voltajes hace una gran diferencia en cómo se suman las cifras. Mientras lee el voltaje en R 1 —R 2 y R 1 —R 2 —R 3 ( Estoy usando un símbolo de “doble guión” “-” para representar la conexión serie entre resistencias R 1 , R 2 y R 3 ), vemos cómo los voltajes miden magnitudes sucesivamente más grandes (aunque negativas), porque las polaridades de las caídas de voltaje individuales están en la misma orientación (positivo a la izquierda, negativo a la derecha). La suma de las caídas de voltaje en R 1 , R 2 y R 3 es igual a 45 voltios, que es lo mismo que la salida de la batería, excepto que La polaridad de la batería es opuesta a la de las caídas de voltaje del resistor (negativo a la izquierda, positivo a la derecha), por lo que terminamos con 0 voltios medidos en toda la cadena de componentes.
Que deberíamos terminar con exactamente 0 voltios en toda la cadena tampoco debería ser un misterio. Al observar el circuito, podemos ver que el extremo izquierdo de la cadena (lado izquierdo de R 1 : punto número 2) está directamente conectado al extremo derecho de la cadena (lado derecho de la batería: número de punto 2), según sea necesario para completar el circuito. Como estos dos puntos están directamente conectados, son eléctricamente comunes entre sí. Y, como tal, el voltaje entre esos dos puntos eléctricamente comunes debe ser cero.
Demostrando la ley de voltaje de Kirchhoff en un circuito paralelo
La Ley de Voltaje de Kirchhoff (a veces denominada KVL para abreviar) funcionará para cualquier configuración de circuito , no solo para series simples. Observe cómo funciona para este circuito paralelo:

Al ser un circuito paralelo, el voltaje en cada resistencia es el mismo que el voltaje de suministro: 6 voltios. Al calcular los voltajes alrededor del bucle 2-3-4-5-6-7-2, obtenemos:

Observe cómo etiqueto el voltaje final (suma) como E 2-2 . Desde que comenzamos nuestra secuencia de pasos en bucle en el punto 2 y terminamos en el punto 2, la suma algebraica de esos voltajes será la misma que el voltaje medido entre el mismo punto (E 2-2 ), cuál de El curso debe ser cero.
La validez de la ley de voltaje de Kirchhoff, independientemente de la topología del circuito
El hecho de que este circuito sea paralelo en lugar de serie no tiene nada que ver con la validez de la Ley de Voltaje de Kirchhoff. Para el caso, el circuito podría ser una “caja negra”, su configuración de componentes completamente oculta a nuestra vista, con solo un conjunto de terminales expuestos para que podamos medir el voltaje entre ellos, y KVL aún sería cierto:

Pruebe cualquier orden de pasos desde cualquier terminal en el diagrama anterior, retrocediendo hasta la terminal original, y encontrará que la suma algebraica de los voltajes siempre es igual a cero.
Además, el “bucle” que rastreamos para KVL ni siquiera tiene que ser una ruta de corriente real en el sentido de circuito cerrado de la palabra. Todo lo que tenemos que hacer para cumplir con KVL es comenzar y terminar en el mismo punto del circuito, contando las caídas de voltaje y las polaridades a medida que avanzamos entre el siguiente y el último punto. Considere este ejemplo absurdo, trazando el “bucle” 2-3-6-3-2 en el mismo circuito de resistencia en paralelo:


Uso de la ley de voltaje de Kirchhoff en un circuito complejo
KVL se puede utilizar para determinar un voltaje desconocido en un circuito complejo, donde se conocen todos los otros voltajes alrededor de un “bucle” particular. Tome como ejemplo el siguiente circuito complejo (en realidad, dos circuitos en serie unidos por un solo cable en la parte inferior):

Para simplificar el problema, he omitido los valores de resistencia y simplemente he dado caídas de voltaje en cada resistencia. Los dos circuitos en serie comparten un cable común entre ellos (cable 7-8-9-10), lo que hace posible las mediciones de voltaje entre los dos circuitos. Si quisiéramos determinar el voltaje entre los puntos 4 y 3, podríamos establecer una ecuación KVL con el voltaje entre esos puntos como desconocido:





Dando la vuelta al bucle 3-4-9-8-3, escribimos las cifras de caída de voltaje como un voltímetro digital las registraría, midiendo con el cable de prueba rojo en el punto de adelante y el cable de prueba negro en el punto de atrás como avanzamos alrededor del ciclo. Por lo tanto, el voltaje del punto 9 al punto 4 es positivo (+) 12 voltios porque el “cable rojo” está en el punto 9 y el “cable negro” está en el punto 4. El voltaje del punto 3 al punto 8 es positivo (+) 20 voltios porque el “cable rojo” está en el punto 3 y el “cable negro” está en el punto 8. El voltaje del punto 8 al punto 9 es cero, por supuesto, porque esos dos puntos son eléctricamente comunes.
Nuestra respuesta final para el voltaje del punto 4 al punto 3 es un negativo (-) 32 voltios, que nos dice que el punto 3 es realmente positivo con respecto al punto 4, precisamente lo que un voltímetro digital indicaría con el cable rojo encendido punto 4 y el plomo negro en el punto 3:
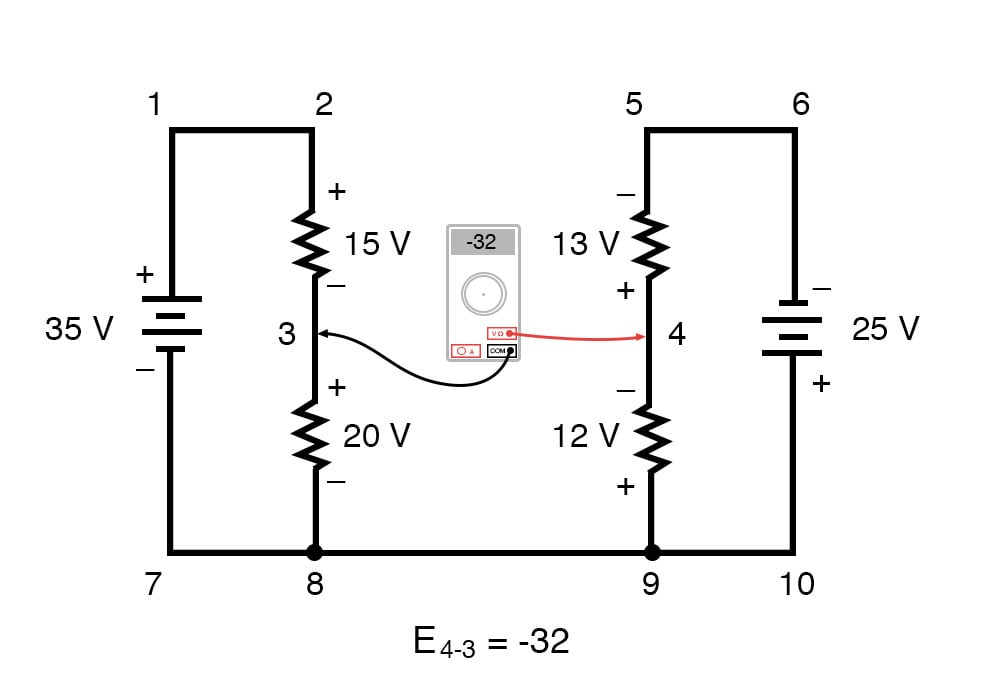
En otras palabras, la ubicación inicial de nuestros “cables del medidor” en este problema de KVL fue “hacia atrás”. Si hubiéramos generado nuestra ecuación KVL comenzando con E 3-4 en lugar de E 4-3 , dando la vuelta al mismo bucle con la orientación de avance del medidor opuesto, la respuesta final habría sido E 3-4 = +32 voltios:

Es importante darse cuenta de que ninguno de los enfoques es “incorrecto”. En ambos casos, llegamos a la evaluación correcta del voltaje entre los dos puntos, 3 y 4: el punto 3 es positivo con respecto al punto 4, y el voltaje entre ellos es de 32 voltios.
REVISIÓN:
- Ley de voltaje de Kirchhoff (KVL): “La suma algebraica de todos los voltajes en un bucle debe ser igual a cero”
HOJAS DE TRABAJO RELACIONADAS: