El descubrimiento de las partes del átomo
El uso científico moderno denota que el átomo está compuesto de partículas constituyentes: el electrón, el protón y el neutrón.
Objetivos de aprendizaje
Discuta los experimentos que llevaron al descubrimiento del electrón y el núcleo
Puntos clave
Puntos clave
- El físico británico J. J. Thomson realizó experimentos para estudiar los rayos catódicos y descubrió que eran partículas únicas, más tarde llamadas electrones.
- Rutherford demostró que el núcleo de hidrógeno está presente en otros núcleos.
- En 1932, James Chadwick demostró que había partículas no cargadas en la radiación que estaba usando. Estas partículas, más tarde llamadas neutrones, tenían una masa similar de los protones pero no tenían las mismas características que los protones.
Términos clave
- centelleo : Un destello de luz producido en un material transparente por el paso de una partícula.
- partícula alfa : núcleo con carga positiva de un átomo de helio-4 (que consta de dos protones y dos neutrones), emitido como consecuencia de la radiactividad.
- cátodo : electrodo a través del cual fluye corriente eléctrica desde un dispositivo eléctrico polarizado.
Aunque originalmente visto como una partícula que no se puede cortar en partículas más pequeñas, el uso científico moderno denota que el átomo está compuesto de varias partículas subatómicas. Las partículas constituyentes de un átomo (cada una descubierta independientemente) son: el electrón, el protón y el neutrón. (Sin embargo, el átomo de hidrógeno-1 no tiene neutrones, y un ion de hidrógeno positivo no tiene electrones).

Modelo atómico clásico : modelo atómico antes del advenimiento de la mecánica cuántica.
Electrón
El físico alemán Johann Wilhelm Hittorf emprendió el estudio de la conductividad eléctrica en gases enrarecidos. En 1869, descubrió un resplandor emitido por el cátodo que aumentó de tamaño con la disminución de la presión de gas. En 1896, el físico británico J. J. Thomson realizó experimentos que demuestran que los rayos catódicos eran partículas únicas, en lugar de ondas, átomos o moléculas, como se creía anteriormente. Thomson hizo buenas estimaciones tanto de la carga [latex] text {e} [/ latex] como de la masa [latex] text {m} [/ latex], encontrando que las partículas de rayos catódicos (que llamó “corpúsculos”) tenían quizás una milésima parte de la masa de hidrógeno, el ion menos masivo conocido. Mostró que su relación carga / masa (e / m) era independiente del material del cátodo. (La figura 1 muestra un haz de electrones desviados).

Haz de electrones : un haz de electrones desviado en un círculo por un campo magnético.
Protón
En 1917 (en experimentos reportados en 1919), Rutherford demostró que el núcleo de hidrógeno está presente en otros núcleos, un resultado generalmente descrito como el descubrimiento del protón. Anteriormente, Rutherford aprendió a crear núcleos de hidrógeno como un tipo de radiación producida como un rendimiento del impacto de las partículas alfa en el gas de hidrógeno; Estos núcleos fueron reconocidos por su firma de penetración única en el aire y su aparición en detectores de centelleo. Estos experimentos comenzaron cuando Rutherford notó que cuando las partículas alfa se disparaban al aire (principalmente nitrógeno), sus detectores de centelleo mostraban las firmas de los núcleos de hidrógeno típicos como producto. Después de la experimentación, Rutherford trazó la reacción al nitrógeno en el aire y descubrió que el efecto era mayor cuando se producían alfa en gas nitrógeno puro. Rutherford determinó que la única fuente posible de este hidrógeno era el nitrógeno y, por lo tanto, el nitrógeno debe contener núcleos de hidrógeno. Un núcleo de hidrógeno fue eliminado por el impacto de la partícula alfa, produciendo oxígeno-17 en el proceso. Esta fue la primera reacción nuclear reportada, [latex] 14 text {N} + alpha rightarrow 17 text {O} + text {p} [/ latex].
Neutron
En 1920, Ernest Rutherford concibió la posible existencia del neutrón. En particular, Rutherford examinó la disparidad encontrada entre el número atómico de un átomo y su masa atómica. Su explicación para esto fue la existencia de una partícula cargada neutralmente dentro del núcleo atómico. Consideró que el neutrón es un doble neutro que consiste en un electrón en órbita alrededor de un protón. En 1932, James Chadwick mostró partículas no cargadas en la radiación que utilizó. Estas partículas tenían una masa similar a la de los protones, pero no tenían las mismas características que los protones. Chadwick siguió algunas de las predicciones de Rutherford, el primero en trabajar en este campo entonces desconocido.
Primeros modelos del átomo
Dalton creía que esa materia está compuesta de unidades discretas llamadas átomos, partículas de materia indivisibles y últimas.
Objetivos de aprendizaje
Describa los postulados de la teoría atómica de Dalton y las teorías atómicas de los filósofos griegos antiguos
Puntos clave
Puntos clave
- El átomo es una unidad básica de materia que consiste en un núcleo central denso rodeado por una nube de electrones cargados negativamente.
- El conocimiento disperso descubierto por los alquimistas durante la Edad Media contribuyó al descubrimiento de los átomos.
- Dalton estableció su teoría atómica basada en el hecho de que las masas de reactivos en reacciones químicas específicas siempre tienen una relación de masa particular.
Términos clave
- fuerza electromagnética : una fuerza fundamental de largo alcance que actúa entre cuerpos cargados, mediada por el intercambio de fotones
- Número de Avogadro : el número de partículas constituyentes (generalmente átomos o moléculas) en un mol de una sustancia determinada. Tiene dimensiones de mol recíproco y su valor es igual a $ 6.02214129 cdot 10 ^ {23} text {mol} ^ {- 1} $
- núcleo : la parte central masiva, cargada positivamente de un átomo, compuesta de protones y neutrones
El átomo es una unidad básica de materia que consiste en un núcleo central denso rodeado por una nube de electrones cargados negativamente. El núcleo atómico contiene una mezcla de protones cargados positivamente y neutrones eléctricamente neutros (excepto en el caso del hidrógeno-1, que es el único nucleido estable sin neutrones). Los electrones de un átomo están unidos al núcleo por la fuerza electromagnética. Tenemos un modelo detallado (y preciso) del átomo ahora, pero nos llevó mucho tiempo encontrar la respuesta correcta.

Ilustración del átomo de helio : Esta es una ilustración del átomo de helio, que representa el núcleo (rosa) y la distribución de la nube de electrones (negro). El núcleo (arriba a la derecha) en helio-4 es en realidad esféricamente simétrico y se parece mucho a la nube de electrones, aunque para núcleos más complicados este no es siempre el caso. La barra negra es un angstrom ([latex] 10 ^ {- 10} [/ latex] m, o 100 pm).
La gente ha especulado durante mucho tiempo sobre la estructura de la materia y la existencia de átomos. Las primeras ideas significativas para sobrevivir son de los antiguos griegos del siglo V a. C., especialmente de los filósofos Leucipo y Demócrito. (Existe cierta evidencia de que los filósofos tanto en India como en China hicieron especulaciones similares aproximadamente al mismo tiempo). Consideraron la cuestión de si una sustancia puede dividirse sin límite en piezas cada vez más pequeñas. Solo hay unas pocas respuestas posibles a esta pregunta. Una es que es posible una subdivisión infinitesimalmente pequeña. Otra es lo que Demócrito en particular creía: que hay una unidad más pequeña que no se puede subdividir más. Demócrito lo llamó el átomo. Ahora sabemos que los átomos en sí pueden subdividirse, pero su identidad se destruye en el proceso, por lo que los griegos tenían razón en un aspecto. Los griegos también sintieron que los átomos estaban en constante movimiento, otra noción correcta.
Los griegos y otros especularon sobre las propiedades de los átomos, y propusieron que solo existían unos pocos tipos y que toda la materia se formaba como varias combinaciones de estos tipos. La famosa propuesta de que los elementos básicos eran tierra, aire, fuego y agua era brillante pero incorrecta. Los griegos habían identificado los ejemplos más comunes de los cuatro estados de la materia (sólido, gas, plasma y líquido) en lugar de los elementos químicos básicos. Pasaron más de 2000 años antes de que se pudieran hacer observaciones con equipos capaces de revelar la verdadera naturaleza de los átomos.
A lo largo de los siglos, se hicieron descubrimientos sobre las propiedades de las sustancias y sus reacciones químicas. Se reconocieron ciertas características sistemáticas, pero las similitudes entre elementos comunes y raros resultaron en esfuerzos para transmutarlos (plomo en oro, en particular) para obtener ganancias financieras. El secreto era un lugar común. Los alquimistas descubrieron y redescubrieron muchos hechos, pero no los hicieron ampliamente disponibles. Cuando terminó la Edad Media, la práctica de la alquimia se desvaneció gradualmente y surgió la ciencia de la química. Ya no era posible, ni se consideraba deseable, mantener los descubrimientos en secreto. El conocimiento colectivo creció y, a principios del siglo XIX , un hecho importante estaba bien establecido: las masas de reactivos en reacciones químicas específicas siempre tienen una relación de masa particular. Esta es una evidencia indirecta muy fuerte de que hay unidades básicas (átomos y moléculas) que tienen estas mismas relaciones de masa. El químico inglés John Dalton (1766-1844) realizó gran parte de este trabajo, con importantes contribuciones del físico italiano Amedeo Avogadro (1776-1856). Fue Avogadro quien desarrolló la idea de un número fijo de átomos y moléculas en un lunar. Este número especial se llama el número de Avogadro en su honor ([latex] 6.022 cdot 10 ^ {23} [/ latex]).
Dalton creía que la materia está compuesta de unidades discretas llamadas átomos, en oposición a la noción obsoleta de que la materia podría dividirse en cualquier cantidad arbitrariamente pequeña. También creía que los átomos son las partículas indivisibles y últimas de la materia. Sin embargo, esta creencia fue anulada cerca del final del siglo 19 por Thomson, con su descubrimiento de electrones.
El modelo de Thomson
Thomson propuso que el átomo está compuesto de electrones rodeados por una sopa de carga positiva para equilibrar las cargas negativas de los electrones.
Objetivos de aprendizaje
Describa el modelo de un átomo propuesto por J. J. Thomson.
Puntos clave
Puntos clave
- J. J. Thomson, quien descubrió el electrón en 1897, propuso el modelo del átomo de ciruela del átomo en 1904 antes del descubrimiento del núcleo atómico para incluir el electrón en el modelo atómico.
- En el modelo de Thomson, el átomo está compuesto de electrones rodeados por una sopa de carga positiva para equilibrar las cargas negativas de los electrones, como “ciruelas” cargadas negativamente rodeadas de “pudín” cargado positivamente.
- El modelo Thomson de 1904 fue refutado por el experimento de la lámina de oro de 1909 de Hans Geiger y Ernest Marsden.
Términos clave
- núcleo : la parte central masiva, cargada positivamente de un átomo, compuesta de protones y neutrones
J. J. Thomson, quien descubrió el electrón en 1897, propuso el modelo de pudín de ciruela del átomo en 1904 antes del descubrimiento del núcleo atómico para incluir el electrón en el modelo atómico. En el modelo de Thomson, el átomo está compuesto de electrones (que Thomson todavía llamaba “corpúsculos”, aunque GJ Stoney había propuesto que los átomos de electricidad se llamaran electrones en 1894) rodeado de una sopa de carga positiva para equilibrar las cargas negativas de los electrones, como “ciruelas” cargadas negativamente rodeadas de “pudín” cargado positivamente. Se pensaba que los electrones (como los conocemos hoy) estaban posicionados en todo el átomo en anillos giratorios. En este modelo, el átomo también se describía a veces como una “nube” de carga positiva.

Modelo del átomo de ciruela del átomo : Una presentación esquemática del modelo del pudín de ciruela del átomo; En el modelo matemático de Thomson, los “corpúsculos” (en el lenguaje moderno, los electrones) estaban dispuestos de forma no aleatoria, en anillos giratorios.
Con este modelo, Thomson abandonó su hipótesis anterior de “átomo nebular”, en la que el átomo estaba compuesto de vórtices inmateriales. Ahora, al menos parte del átomo debía estar compuesto por los corpúsculos negativos de partículas de Thomson, aunque el resto de la parte cargada positivamente del átomo permaneció algo nebuloso y mal definido.
El modelo Thomson de 1904 fue refutado por el experimento de la lámina de oro de 1909 realizado por Hans Geiger y Ernest Marsden. Este experimento de lámina de oro fue interpretado por Ernest Rutherford en 1911 para sugerir que hay un núcleo muy pequeño del átomo que contiene una carga positiva muy alta (en el caso del oro, suficiente para equilibrar la carga negativa colectiva de aproximadamente 100 electrones). Sus conclusiones lo llevaron a proponer el modelo de Rutherford del átomo.
El modelo de Rutherford
Rutherford confirmó que el átomo tenía un centro concentrado de carga positiva y una masa relativamente grande.
Objetivos de aprendizaje
Describa el experimento de la lámina de oro realizado por Geiger y Marsden bajo las instrucciones de Rutherford y sus implicaciones para el modelo del átomo
Puntos clave
Puntos clave
- Rutherford volcó el modelo de Thomson en 1911 con su conocido experimento de lámina de oro, en el que demostró que el átomo tiene un pequeño núcleo de gran masa.
- En su experimento, Rutherford observó que muchas partículas alfa se desviaban en ángulos pequeños mientras que otras se reflejaban de nuevo en la fuente alfa.
- Esta región altamente concentrada y cargada positivamente se denomina “núcleo” del átomo.
Términos clave
- partícula alfa : un núcleo cargado positivamente de un átomo de helio-4 (que consta de dos protones y dos neutrones), emitido como consecuencia de la radiactividad; Partícula α.
El modelo de Rutherford es un modelo del átomo que lleva el nombre de Ernest Rutherford. Rutherford dirigió el famoso experimento Geiger-Marsden en 1909, que sugirió, según el análisis de Rutherford de 1911, que el llamado “modelo de pudín de ciruela” del átomo de J. J. Thomson era incorrecto. El nuevo modelo de Rutherford para el átomo, basado en los resultados experimentales, contenía las nuevas características de una carga central relativamente alta concentrada en un volumen muy pequeño en comparación con el resto del átomo. Este volumen central también contenía la mayor parte de la masa del átomo. Esta región más tarde se llamaría el “núcleo”. “

Modelo planetario atómico : Diagrama básico del modelo planetario atómico; los electrones están en verde y el núcleo está en rojo
En 1911, Rutherford diseñó un experimento para explorar más la estructura atómica utilizando las partículas alfa emitidas por un elemento radiactivo. Siguiendo su dirección, Geiger y Marsden dispararon partículas alfa con grandes energías cinéticas hacia una delgada lámina de oro. Se esperaba que la medición del patrón de partículas dispersas proporcionara información sobre la distribución de carga dentro del átomo. Según el modelo predominante de pudín de ciruela, las partículas alfa deberían haberse desviado, como máximo, unos pocos grados. Sin embargo, los resultados reales sorprendieron a Rutherford. Aunque muchas de las partículas alfa pasaron como se esperaba, muchas otras fueron desviadas en ángulos pequeños, mientras que otras se reflejaron en la fuente alfa.
A partir de consideraciones puramente energéticas de hasta qué punto las partículas de velocidad conocida podrían penetrar hacia una carga central de 100 e, Rutherford pudo calcular que el radio de su carga central de oro tendría que ser menor que [látex] 3.4 cdot 10 ^ {- 14} [/ latex] metros. Esto estaba en un átomo de oro que se sabe que tiene aproximadamente [látex] 10 ^ {- 10} [/ látex] metros de radio; un hallazgo muy sorprendente, ya que implicaba una fuerte carga central menor que [látex] frac {1} {3000} [/ látex] th del diámetro del átomo.
El modelo de Bohr del átomo
Bohr sugirió que los electrones en el hidrógeno podrían tener ciertos movimientos clásicos solo cuando están restringidos por una regla cuántica .
Objetivos de aprendizaje
Describa el modelo de átomo propuesto por Niels Bohr.
Puntos clave
Puntos clave
- Según Bohr: 1) Los electrones en los átomos orbitan alrededor del núcleo, 2) Los electrones solo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas, y 3) Los electrones solo pueden ganar y perder energía al saltar de una órbita permitida a otra .
- La importancia del modelo de Bohr es que las leyes de la mecánica clásica se aplican al movimiento del electrón alrededor del núcleo solo cuando están restringidas por una regla cuántica. Por lo tanto, su modelo atómico se llama modelo semiclásico.
- Las leyes de la mecánica clásica predicen que el electrón debería liberar radiación electromagnética mientras orbita un núcleo, lo que sugiere que todos los átomos deberían ser inestables.
Términos clave
- Ecuaciones de Maxwell : Un conjunto de ecuaciones que describen cómo los campos eléctricos y magnéticos son generados y alterados entre sí y por cargas y corrientes.
- semiclásico : una teoría en la que una parte de un sistema se describe con mecánica cuántica mientras que la otra se trata de manera clásica.
El modelo de Bohr del átomo
El gran físico danés Niels Bohr (1885–1962) hizo uso inmediato del modelo planetario del átomo de Rutherford. Bohr se convenció de su validez y pasó parte de 1912 en el laboratorio de Rutherford. En 1913, después de regresar a Copenhague, comenzó a publicar su teoría del átomo más simple, el hidrógeno, basada en el modelo planetario del átomo.

Niels Bohr : Niels Bohr, físico danés, utilizó el modelo planetario del átomo para explicar el espectro atómico y el tamaño del átomo de hidrógeno. Sus numerosas contribuciones al desarrollo de la física atómica y la mecánica cuántica; su influencia personal en muchos estudiantes y colegas; y su integridad personal, especialmente frente a la opresión nazi, le valió un lugar destacado en la historia. (crédito: Autor desconocido, a través de Wikimedia Commons)
Durante décadas, se hicieron muchas preguntas sobre las características atómicas. Desde sus tamaños hasta sus espectros, se sabía mucho sobre los átomos, pero poco se había explicado en términos de las leyes de la física. La teoría de Bohr explicó el espectro atómico del hidrógeno, lo hizo instantáneamente famoso y estableció principios nuevos y ampliamente aplicables en mecánica cuántica.
Un gran rompecabezas que tenía el modelo planetario del átomo era el siguiente. Las leyes de la mecánica clásica predicen que el electrón debería liberar radiación electromagnética mientras orbita un núcleo (según las ecuaciones de Maxwell, la carga acelerada debería emitir radiación electromagnética). Debido a que el electrón perdería energía, gradualmente iría en espiral hacia adentro, colapsando en el núcleo. Este modelo atómico es desastroso, porque predice que todos los átomos son inestables. Además, a medida que el electrón gira en espiral hacia adentro, la emisión aumentaría gradualmente en frecuencia a medida que la órbita se hiciera más pequeña y más rápida. Esto produciría una mancha continua, en frecuencia, de radiación electromagnética. Sin embargo, los experimentos de finales del siglo XIX con descargas eléctricas han demostrado que los átomos solo emitirán luz (es decir, radiación electromagnética) a ciertas frecuencias discretas.
Para superar esta dificultad, Niels Bohr propuso, en 1913, lo que ahora se llama el modelo de Bohr del átomo. Sugirió que los electrones solo podían tener ciertos movimientos clásicos:
- Los electrones en los átomos orbitan el núcleo.
- Los electrones solo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (llamadas por Bohr las “órbitas estacionarias”): en un cierto conjunto discreto de distancias desde el núcleo. Estas órbitas están asociadas con energías definidas y también se llaman capas de energía o niveles de energía. En estas órbitas, la aceleración del electrón no produce radiación y pérdida de energía como lo requiere la electrodinámica clásica.
- Los electrones solo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia [látex] nu [/ látex] determinada por la diferencia de energía de los niveles según la relación de Planck:
[látex] Delta { text {E}} = text {E} _2- text {E} _1 = text {h} nu , [/ latex]
donde [latex] text {h} [/ latex] es la constante de Planck y [latex] nu [/ latex] es la frecuencia de la radiación.
Modelo semiclásico
La importancia del modelo de Bohr es que las leyes de la mecánica clásica se aplican al movimiento del electrón alrededor del núcleo solo cuando están restringidas por una regla cuántica . Por lo tanto, su modelo atómico se llama modelo semiclásico.
Suposiciones básicas del modelo de Bohr
Bohr explicó el espectro de hidrógeno con éxito al adoptar una condición de cuantificación e introducir la constante de Planck en su modelo.
Objetivos de aprendizaje
Describa los supuestos básicos que Niels Bohr aplicó al modelo planetario de un átomo
Puntos clave
Puntos clave
- La electrodinámica clásica predice que un átomo descrito por un modelo planetario (clásico) sería inestable.
- Para explicar el espectro de hidrógeno, Bohr tuvo que hacer algunas suposiciones de que los electrones solo podían tener ciertos movimientos clásicos.
- Después del trabajo seminal de Planck, Einstein y Bohr, los físicos comenzaron a darse cuenta de que era esencial introducir la noción de “cuantización” para explicar mundos microscópicos.
Términos clave
- cuerpo negro : un cuerpo físico idealizado que absorbe toda la radiación electromagnética incidente, independientemente de la frecuencia o el ángulo de incidencia. Aunque el cuerpo negro es un concepto teórico, puede encontrar realizaciones aproximadas del cuerpo negro en la naturaleza.
- efecto fotoeléctrico : La aparición de electrones emitidos por la materia (metales y sólidos, líquidos o gases no metálicos) como consecuencia de su absorción de energía de la radiación electromagnética.
En módulos anteriores, hemos visto rompecabezas de teorías atómicas clásicas (por ejemplo, el modelo de Rutherford). Lo más importante, la electrodinámica clásica predice que un átomo descrito por un modelo planetario (clásico) sería inestable. Para explicar el rompecabezas, Bohr propuso lo que ahora se llama el modelo de Bohr del átomo en 1913. Sugirió que los electrones solo podrían tener ciertos movimientos clásicos:
- Los electrones en los átomos orbitan el núcleo.
- Los electrones solo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (llamadas por Bohr las “órbitas estacionarias”) en un cierto conjunto discreto de distancias desde el núcleo. Estas órbitas están asociadas con energías definidas y también se llaman capas de energía o niveles de energía. En estas órbitas, la aceleración del electrón no produce radiación y pérdida de energía como lo requiere la electrodinámica clásica.
- Los electrones solo pueden ganar y perder energía saltando de una órbita permitida a otra, absorbiendo o emitiendo radiación electromagnética con una frecuencia [látex] nu [/ látex] determinada por la diferencia de energía de los niveles según la relación de Planck: [latex] Delta { text {E}} = text {E} _2- text {E} _1 = text {h} nu [/ latex], donde [latex] text {h} [/ latex] es la constante de Planck. Además, Bohr también asumió que el momento angular [latex] text {L} [/ latex] está restringido a ser un múltiplo entero de una unidad fija: [latex] text {L} = text {n} { text {h} over 2 pi} = text {n} hbar [/ latex], donde [latex] text {n} = 1, 2, 3, dots [/ latex] se denomina cuántico principal número y [latex] hbar = frac { text {h}} {2 pi} [/ latex].
Hemos visto que Planck adoptó una nueva condición de cuantificación de energía para explicar la radiación del cuerpo negro, donde introdujo la constante de Planck [latex] text {h} [/ latex] por primera vez. Poco después, Einstein recurrió a este nuevo concepto de cuantificación de energía y usó la constante de Planck nuevamente para explicar los efectos fotoeléctricos, en los cuales asumió que la radiación electromagnética interactúa con la materia como partículas (más tarde llamadas “fotones”). Aquí, Bohr explicó el espectro de hidrógeno atómico con éxito por primera vez adoptando una condición de cuantificación e introduciendo la constante de Planck en su modelo atómico. Durante el período de desarrollo radical a principios del siglo XX , los físicos comenzaron a darse cuenta de que era esencial introducir la noción de “cuantización” para explicar mundos microscópicos.

Modelo Rutherford-Bohr : El modelo Rutherford – Bohr del átomo de hidrógeno ([látex] text {Z} = 1 [/ látex]) o un ion similar al hidrógeno ([látex] texto {Z}> 1 [/ latex]), donde el electrón cargado negativamente confinado a una capa atómica rodea un pequeño núcleo atómico cargado positivamente, y donde un salto de electrones entre órbitas está acompañado por una cantidad de energía electromagnética emitida o absorbida ( [látex] text {h} nu [/ latex]). Las órbitas en las que puede viajar el electrón se muestran como círculos grises; su radio aumenta a medida que [latex] text {n} ^ 2 [/ latex], donde [latex] text {n} [/ latex] es el número cuántico principal. La transición [latex] 3 rightarrow 2 [/ latex] representada aquí produce la primera línea de la serie Balmer, y para el hidrógeno ([latex] text {Z} = 1 [/ latex]) produce un fotón de longitud de onda 656 nm (luz roja).
Órbitas de Bohr
Según Bohr, los electrones solo pueden orbitar de manera estable, en ciertas órbitas, a un cierto conjunto discreto de distancias desde el núcleo.
Objetivos de aprendizaje
Explique la relación entre las “órbitas de Bohr” y el efecto de cuantificación
Puntos clave
Puntos clave
- Las “órbitas de Bohr” tienen una característica muy importante de la cuantización: que el momento angular L de un electrón en su órbita está cuantificado, es decir, solo tiene valores específicos y discretos. Esto lleva a la ecuación L = mevrn = nℏL = m_e v r_n = n hbar.
- En el momento de la propuesta, el propio Bohr no sabía por qué debería cuantificarse el momento angular, pero utilizando esta suposición fue capaz de calcular las energías en el espectro de hidrógeno.
- Una teoría del átomo o de cualquier otro sistema debe predecir sus energías basándose en la física del sistema, que el modelo de Bohr pudo hacer.
Términos clave
- cuantización : El proceso de explicar una comprensión clásica de los fenómenos físicos en términos de una comprensión más nueva conocida como mecánica cuántica.
El físico danés Neils Bohr fue lo suficientemente inteligente como para descubrir un método para calcular las energías orbitales de los electrones en el hidrógeno. Como hemos visto en el módulo anterior “El modelo de átomo de Bohr”, Bohr asumió que los electrones solo pueden orbitar de manera estable, sin irradiar, en ciertas órbitas (llamadas por Bohr como “órbitas estacionarias”), en un cierto conjunto discreto de distancias desde el núcleo. Estas “órbitas de Bohr” tienen una característica muy importante de cuantización como se muestra a continuación. Este fue un primer paso importante que se ha mejorado, pero vale la pena repetirlo aquí, ya que describe correctamente muchas características del hidrógeno. Suponiendo órbitas circulares, Bohr propuso que el momento angular [latex] text {L} [/ latex] de un electrón en su órbita se cuantifica, es decir, tiene solo valores específicos y discretos. El valor para [latex] text {L} [/ latex] viene dado por la fórmula:
[látex] displaystyle text {L} = text {m} _ text {e} text {v} text {r} _ text {n} = text {n} { text {h} over 2 pi} = text {n} hbar [/ latex]
donde [latex] text {L} [/ latex] es el momento angular, [latex] text {m} _ text {e} [/ latex] es la masa del electrón, [latex] text { r} _ text {n} [/ latex] es el radio de la [órbita latex] text {n} [/ latex], y [latex] text {h} [/ latex] es la constante de Planck. Tenga en cuenta que el momento angular es [látex] text {L} = text {I} omega [/ latex]. Para un objeto pequeño en un radio [latex] text {r} [/ latex], [latex] text {I} = text {mr} ^ 2 [/ latex] y [latex] omega = frac { text {v}} { text {r}} [/ latex], de modo que:
[látex] displaystyle text {L} = ( text {mr} ^ 2) ( frac { text {v}} { text {r}}) = text {mvr} [/ latex ]
La cuantización dice que este valor de [latex] text {mvr} [/ latex] solo puede tener valores discretos. En ese momento, el propio Bohr no sabía por qué debería cuantificarse el momento angular, pero utilizando esta suposición fue capaz de calcular las energías en el espectro de hidrógeno, algo que nadie más había hecho en ese momento.
A continuación se muestra un diagrama de nivel de energía, que es una forma conveniente de mostrar estados de energía: los niveles de energía permitidos del electrón (en relación con nuestra discusión). La energía se traza verticalmente con el estado más bajo o fundamental en la parte inferior y con los estados excitados arriba. Dadas las energías de las líneas en un espectro atómico, es posible (aunque a veces muy difícil) determinar los niveles de energía de un átomo. Los diagramas de nivel de energía se utilizan para muchos sistemas, incluidas las moléculas y los núcleos. Una teoría del átomo o de cualquier otro sistema debe predecir sus energías en función de la física del sistema.
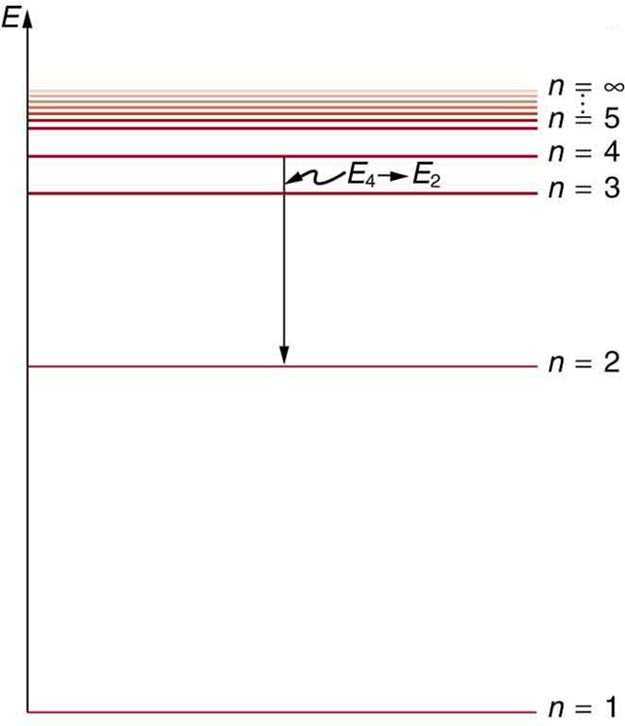
Diagrama de diagrama de nivel de energía : Un diagrama de nivel de energía traza la energía verticalmente y es útil para visualizar los estados de energía de un sistema y las transiciones entre ellos. Este diagrama es para los electrones del átomo de hidrógeno, que muestra una transición entre dos órbitas que tienen energías [látex] text {E} _4 [/ latex] y [latex] text {E} _2 [/ latex].
Energía de una órbita de Bohr
Basado en sus suposiciones, Bohr obtuvo varias propiedades importantes del átomo de hidrógeno de la física clásica.
Objetivos de aprendizaje
Aplica la ecuación adecuada para calcular los niveles de energía y la energía de un fotón emitido para un átomo similar al hidrógeno
Puntos clave
Puntos clave
- Según Bohr, el radio de órbita permitido en cualquier [latex] text {n} [/ latex] es [latex] text {r} _ text {n} = { text {n} ^ 2 hbar ^ 2 over text {Zk} _ text {e} text {e} ^ 2 text {m} _ text {e}} [/ latex]. The smallest possible value of [latex]text{r}[/latex] in the hydrogen atom is called the Bohr radius and is equal to 0.053 nm.
- The energy of the [latex]text{n}[/latex]-th level for any atom is [latex]text{E} = approx {-13.6text{Z}^2 over text{n}^2}mathrm{text{eV}}[/latex].
- The energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels: [latex]text{E}=text{E}_text{i}-text{E}_text{f}=text{R} left( frac{1}{text{n}_{text{f}}^2} – frac{1}{text{n}_{text{i}}^2} right) ,[/latex], which is known as Rydberg formula.
Términos clave
- centripetal : Directed or moving towards a center.
From Bohr’s assumptions, we will now derive a number of important properties of the hydrogen atom from the classical physics. We start by noting the centripetal force causing the electron to follow a circular path is supplied by the Coulomb force. To be more general, we note that this analysis is valid for any single-electron atom. So, if a nucleus has [latex]text{Z}[/latex] protons ([latex]text{Z}=1[/latex] for hydrogen, [latex]text{Z}=2[/latex] for helium, etc.) and only one electron, that atom is called a hydrogen-like atom.
The spectra of hydrogen-like ions are similar to hydrogen, but shifted to higher energy by the greater attractive force between the electron and nucleus. The magnitude of the centripetal force is [latex]frac{text{m}_text{ev}^2}{text{r}_text{n}}[/latex], while the Coulomb force is [latex]frac{text{Zk}_text{e} text{e}^2}{text{r}^2}[/latex]. The tacit assumption here is that the nucleus is more massive than the stationary electron, and the electron orbits about it. This is consistent with the planetary model of the atom. Equating these:
[latex]displaystyle frac{text{m}_text{e} text{v}^2}{text{r}} = frac{text{Zk}_text{e} text{e}^2}{text{r}^2}[/latex]
This equation determines the electron’s speed at any radius:
[latex]displaystyle text{v} = frac{sqrt{text{Zk}_text{e} text{e}^2}}{text{m}_text{e} text{r}}[/latex]
It also determines the electron’s total energy at any radius:
[latex]displaystyle text{E}= frac{1}{2} text{m}_text{e} text{v}^2 – frac{text{Z} text{k}_text{e} text{e}^2}{text{r}} = – frac{text{Z} text{k}_text{e} text{e}^2}{2text{r}}[/latex]
The total energy is negative and inversely proportional to [latex]text{r}[/latex]. This means that it takes energy to pull the orbiting electron away from the proton. For infinite values of [latex]text{r}[/latex], the energy is zero, corresponding to a motionless electron infinitely far from the proton.
Now, here comes the Quantum rule: As we saw in the previous module, the angular momentum [latex]text{L} = text{m}_text{e} text{r} text{v}[/latex] is an integer multiple of [latex]hbar[/latex]:
[latex]text{m}_text{e} text{v} text{r} = text{n} hbar[/latex]
Substituting the expression in the equation for speed above gives an equation for [latex]text{r}[/latex] in terms of [latex]text{n}[/latex]:
[latex]sqrt{text{Zk}_text{e} text{e}^2 text{m}_text{e} text{r}} = text{n} hbar[/latex]
The allowed orbit radius at any n is then:
[latex]displaystyle text{r}_text{n} = {text{n}^2hbar^2over text{Zk}_text{e} text{e}^2 text{m}_text{e}}[/latex]
The smallest possible value of [latex]text{r}[/latex] in the hydrogen atom is called the Bohr radius and is equal to 0.053 nm. The energy of the [latex]text{n}[/latex]-th level for any atom is determined by the radius and quantum number:
[latex]displaystyle text{E} = -frac{text{Zk}_text{e} text{e}^2}{2text{r}_text{n} } = – frac{ text{Z}^2(text{k}_text{e} text{e}^2)^2 text{m}_text{e} }{2hbar^2 text{n}^2} approx frac{-13.6text{Z}^2}{text{n}^2}mathrm{text{eV}}[/latex]
Using this equation, the energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels:
[latex]displaystyle text{E}=text{E}_text{i}-text{E}_text{f}=text{R} left( frac{1}{text{n}_{text{f}}^2} – frac{1}{text{n}_{text{i}}^2} right)[/latex]
Which is the Rydberg formula describing all the hydrogen spectrum and [latex]text{R}[/latex] is the Rydberg constant. Bohr’s model predicted experimental hydrogen spectrum extremely well.
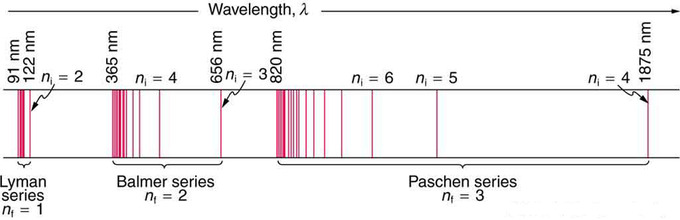
Fig 1 : A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the UV, and the Paschen series and others are in the IR. Values of nf and ni are shown for some of the lines.
Hydrogen Spectra
The observed hydrogen-spectrum wavelengths can be calculated using the following formula: [latex]frac{1}{lambda} = text{R}(frac{1}{text{n}_text{f} ^2} – frac{1}{text{n}_text{i} ^2})[/latex].
Objetivos de aprendizaje
Explain difference between Lyman, Balmer, and Paschen series
Puntos clave
Puntos clave
- Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized).
- Lyman, Balmer, and Paschen series are named after early researchers who studied them in particular depth.
- Bohr was the first one to provide a theoretical explanation of the hydrogen spectra.
Términos clave
- photon : The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.
- spectrum : A condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism.
For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized). Maxwell and others had realized that there must be a connection between the spectrum of an atom and its structure, something like the resonant frequencies of musical instruments. But, despite years of efforts by many great minds, no one had a workable theory. (It was a running joke that any theory of atomic and molecular spectra could be destroyed by throwing a book of data at it, so complex were the spectra.) Following Einstein’s proposal of photons with quantized energies directly proportional to their wavelengths, it became even more evident that electrons in atoms can exist only in discrete orbits.
In some cases, it had been possible to devise formulas that described the emission spectra. As you might expect, the simplest atom—hydrogen, with its single electron—has a relatively simple spectrum. The hydrogen spectrum had been observed in the infrared (IR), visible, and ultraviolet (UV), and several series of spectral lines had been observed. The observed hydrogen-spectrum wavelengths can be calculated using the following formula:
[latex]displaystyle frac{1}{lambda} = text{R}(frac{1}{text{n}_text{f} ^2} – frac{1}{text{n}_text{i} ^2})[/latex]
where [latex]lambda[/latex] is the wavelength of the emitted EM radiation and [latex]text{R}[/latex] is the Rydberg constant, determined by the experiment to be [latex]text{R}=1.097cdot 10^7 text{text{m}}^{-1}[/latex], and [latex]text{n}_text{f}[/latex], [latex]text{n}_text{i}[/latex] are positive integers associated with a specific series.
These series are named after early researchers who studied them in particular depth. For the Lyman series, [latex]text{n}_text{f} = 1[/latex] for the Balmer series, [latex]text{n}_text{f} = 2[/latex]; for the Paschen series, [latex]text{n}_text{f} = 3[/latex]; y así. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as [latex]text{n}_text{f}[/latex] increases. The constant [latex]text{n}_text{i}[/latex] is a positive integer, but it must be greater than [latex]text{n}_text{f}[/latex]. Thus, for the Balmer series, [latex]text{n}_text{f} = 2[/latex] and [latex]text{n}_text{i} = 3,4,5,6…[/latex]. Note that [latex]text{n}_text{i}[/latex] can approach infinity.

Electron transitions and their resulting wavelengths for hydrogen. : Energy levels are not to scale.
While the formula in the wavelengths equation was just a recipe designed to fit data and was not based on physical principles, it did imply a deeper meaning. Balmer first devised the formula for his series alone, and it was later found to describe all the other series by using different values of [latex]text{n}_text{f}[/latex]. Bohr was the first to comprehend the deeper meaning. Again, we see the interplay between experiment and theory in physics. Experimentally, the spectra were well established, an equation was found to fit the experimental data, but the theoretical foundation was missing.
de Broglie and the Bohr Model
By assuming that the electron is described by a wave and a whole number of wavelengths must fit, we derive Bohr’s quantization assumption.
Objetivos de aprendizaje
Describe reinterpretation of Bohr’s condition by de Broglie
Puntos clave
Puntos clave
- Bohr’s condition, that the angular momentum is an integer multiple of [latex]hbar[/latex], was later reinterpreted in 1924 by de Broglie as a standing wave condition.
- For what Bohr was forced to hypothesize as the rule for allowed orbits, de Broglie’s matter wave concept explains it as the condition for constructive interference of an electron in a circular orbit.
- Bohr’s model was only applicable to hydrogen-like atoms. In 1925, more general forms of description (now called quantum mechanics ) emerged, thanks to Heisenberg and Schrodinger.
Términos clave
- standing wave : A wave form which occurs in a limited, fixed medium in such a way that the reflected wave coincides with the produced wave. A common example is the vibration of the strings on a musical stringed instrument.
- matter wave : A concept reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie.
Bohr’s condition, that the angular momentum is an integer multiple of [latex]hbar[/latex], was later reinterpreted in 1924 by de Broglie as a standing wave condition. The wave-like properties of matter were subsequently confirmed by observations of electron interference when scattered from crystals. Electrons can exist only in locations where they interfere constructively. How does this affect electrons in atomic orbits? When an electron is bound to an atom, its wavelength must fit into a small space, something like a standing wave on a string.
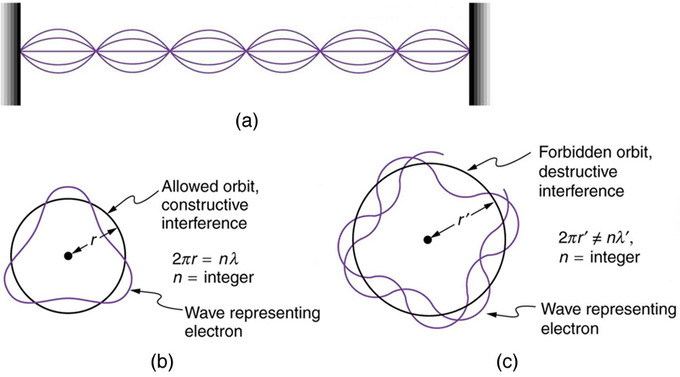
Waves on a String : (a) Waves on a string have a wavelength related to the length of the string, allowing them to interfere constructively. (b) If we imagine the string bent into a closed circle, we get a rough idea of how electrons in circular orbits can interfere constructively. (c) If the wavelength does not fit into the circumference, the electron interferes destructively; it cannot exist in such an orbit.
Allowed orbits are those in which an electron constructively interferes with itself. Not all orbits produce constructive interference and thus only certain orbits are allowed (i.e., the orbits are quantized). By assuming that the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron’s orbit, we have the equation:
[latex]text{n}lambda =2pi text{r}[/latex]
Substituting de Broglie’s wavelength of [latex]frac{text{h}}{text{p}}[/latex] reproduces Bohr’s rule. Since [latex]lambda = text{h}/text{m}_text{ev}[/latex], we now have:
[latex]displaystyle frac{text{nh}}{text{m}_text{ev}} = 2pi text{r}_text{n}[/latex]
Rearranging terms, and noting that [latex]text{L}=text{mvr}[/latex] for a circular orbit, we obtain the quantization of angular momentum as the condition for allowed orbits:
[latex]displaystyle text{L} = text{m}_text{e} text{v} text{r}_text{n} = text{n} frac{text{h}}{2pi}, (text{n}=1,2,3…)[/latex]
As previously stated, Bohr was forced to hypothesize this rule for allowed orbits. We now realize this as the condition for constructive interference of an electron in a circular orbit.
Accordingly, a new kind of mechanics, quantum mechanics, was proposed in 1925. Bohr’s model of electrons traveling in quantized orbits was extended into a more accurate model of electron motion. The new theory was proposed by Werner Heisenberg. By different reasoning, another form of the same theory, wave mechanics, was discovered independently by Austrian physicist Erwin Schrödinger. Schrödinger employed de Broglie’s matter waves, but instead sought wave solutions of a three-dimensional wave equation. This described electrons that were constrained to move about the nucleus of a hydrogen-like atom by being trapped by the potential of the positive nuclear charge.
X-Rays and the Compton Effect
Compton explained the X-ray frequency shift during the X-ray/electron scattering by attributing particle-like momentum to “photons”.
Objetivos de aprendizaje
Describe Compton effects between electrons and x-ray photons
Puntos clave
Puntos clave
- Compton derived the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays.
- Compton effects (with electrons) usually occur with x-ray photons.
- If the photon is of lower energy, in the visible light through soft X-rays range, photoelectric effects are observed. Higher energy photons, in the gamma ray range, may lead to pair production.
Términos clave
- gamma ray : A very high frequency (and therefore very high energy) electromagnetic radiation emitted as a consequence of radioactivity.
- photoelectric effects : In photoelectric effects, electrons are emitted from matter (metals and non-metallic solids, liquids or gases) as a consequence of their absorption of energy from electromagnetic radiation.
- photon : The quantum of light and other electromagnetic energy, regarded as a discrete particle having zero rest mass, no electric charge, and an indefinitely long lifetime.
By the early 20th century, research into the interaction of X-rays with matter was well underway. It was observed that when X-rays of a known wavelength interact with atoms, the X-rays are scattered through an angle [latex]theta[/latex] and emerge at a different wavelength related to [latex]theta[/latex]. Although classical electromagnetism predicted that the wavelength of scattered rays should be equal to the initial wavelength, multiple experiments had found that the wavelength of the scattered rays was longer (corresponding to lower energy) than the initial wavelength.
In 1923, Compton published a paper in the Physical Review which explained the X-ray shift by attributing particle-like momentum to “photons,” which Einstein had invoked in his Nobel prize winning explanation of the photoelectric effect. First postulated by Planck, these “particles” conceptualized “quantized” elements of light as containing a specific amount of energy depending only on the frequency of the light. In his paper, Compton derived the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays by assuming that each scattered X-ray photon interacted with only one electron. His paper concludes by reporting on experiments which verified his derived relation:
[latex]displaystyle lambda’ – lambda = frac{text{h}}{text{m}_text{e} text{c}}(1-cos{theta})[/latex]
where λlambda is the initial wavelength, λ′lambda’ is the wavelength after scattering, [latex]text{h}[/latex] is the Planck constant, mem_e is the Electron rest mass, [latex]text{c}[/latex] is the speed of light, and θtheta is the scattering angle. The quantity hmecfrac{h}{m_e c} is known as the Compton wavelength of the electron; it is equal to [latex]2.43cdot 10^{-12}[/latex] m. The wavelength shift [latex]lambda ‘ – lambda[/latex] is at least zero (for [latex]theta = 0[/latex]°) and at most twice the Compton wavelength of the electron (for [latex]theta = 180[/latex]°). (The derivation of Compton’s formula is a bit lengthy and will not be covered here.)

A Photon Colliding with a Target at Rest : A photon of wavelength [latex]lambda[/latex] comes in from the left, collides with a target at rest, and a new photon of wavelength [latex]lambda ‘[/latex] emerges at an angle [latex]theta[/latex].
Because the mass-energy and momentum of a system must both be conserved, it is not generally possible for the electron simply to move in the direction of the incident photon. The interaction between electrons and high energy photons (comparable to the rest energy of the electron, 511 keV) results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the scattered photon still has enough energy left, the Compton scattering process may be repeated. In this scenario, the electron is treated as free or loosely bound. Photons with an energy of this order of magnitude are in the x-ray range of the electromagnetic radiation spectrum. Therefore, you can say that Compton effects (with electrons) occur with x-ray photons.
If the photon is of lower energy, but still has sufficient energy (in general a few eV to a few keV, corresponding to visible light through soft X-rays), it can eject an electron from its host atom entirely (a process known as the photoelectric effect), instead of undergoing Compton scattering. Higher energy photons (1.022 MeV and above, in the gamma ray range) may be able to bombard the nucleus and cause an electron and a positron to be formed, a process called pair production.
X-Ray Spectra: Origins, Diffraction by Crystals, and Importance
X-ray shows its wave nature when radiated upon atomic/molecular structures and can be used to study them.
Objetivos de aprendizaje
Describe interactions between X-rays and atoms
Puntos clave
Puntos clave
- X rays are relatively high- frequency EM radiation. They are produced by transitions between inner-shell electron levels, which produce x rays characteristic of the atomic element, or by accelerating electrons.
- x-ray diffraction is a technique that provides the detailed information about crystallographic structure of natural and manufactured materials.
- Current research in material science and physics involves complex materials whose lattice arrangements are crucial to obtaining a superconducting material, which can be studied using x-ray crystallography.
Términos clave
- double-helix structure : The structure formed by double-stranded molecules of nucleic acids such as DNA and RNA.
- crystallography : The experimental science of determining the arrangement of atoms in solids.
- diffraction : The bending of a wave around the edges of an opening or an obstacle.
In a previous Atom on X-rays, we have seen that there are two processes by which x-rays are produced in the anode of an x-ray tube. In one process, the deceleration of electrons produces x-rays, and these x-rays are called Bremsstrahlung , or braking radiation. The second process is atomic in nature and produces characteristic x-rays, so called because they are characteristic of the anode material. The x-ray spectrum in is typical of what is produced by an x-ray tube, showing a broad curve of Bremsstrahlung radiation with characteristic x-ray peaks on it.
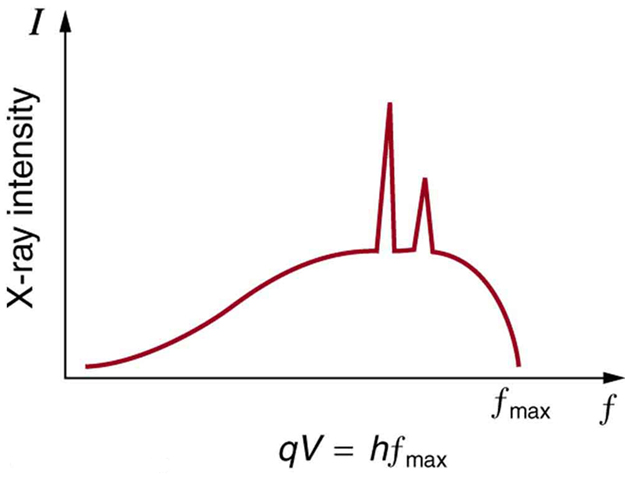
X-Ray Spectrum : X-ray spectrum obtained when energetic electrons strike a material, such as in the anode of a CRT. The smooth part of the spectrum is bremsstrahlung radiation, while the peaks are characteristic of the anode material. A different anode material would have characteristic x-ray peaks at different frequencies.
Since x-ray photons are very energetic, they have relatively short wavelengths. For example, the 54.4-keV Kα x-ray, for example, has a wavelength [latex]lambda = frac{text{hc}}{text{E}} = 0.0228[/latex] nm. Thus, typical x-ray photons act like rays when they encounter macroscopic objects, like teeth, and produce sharp shadows. However, since atoms and atomic structures have a typical size on the order of 0.1 nm, x-ray shows its wave nature with them. The process is called x-ray diffraction because it involves the diffraction and interference of x-rays to produce patterns that can be analyzed for information about the structures that scattered the x-rays.
Shown below, Bragg’s Law gives the angles for coherent and incoherent scattering of light from a crystal lattice, which happens during x-ray diffraction. When x-ray are incident on an atom, they make the electronic cloud move as an electromagnetic wave. The movement of these charges re-radiate waves with the same frequency. This is called Rayleigh Scattering, which you should remember from a previous atom. A similar thing happens when neutron waves from the nuclei scatter from interaction with an unpaired electron. These re-emitted wave fields interfere with each other either constructively or destructively, and produce a diffraction pattern that is captured by a sensor or film. This is called the Braggs diffraction, and is the basis for x-ray diffraction.
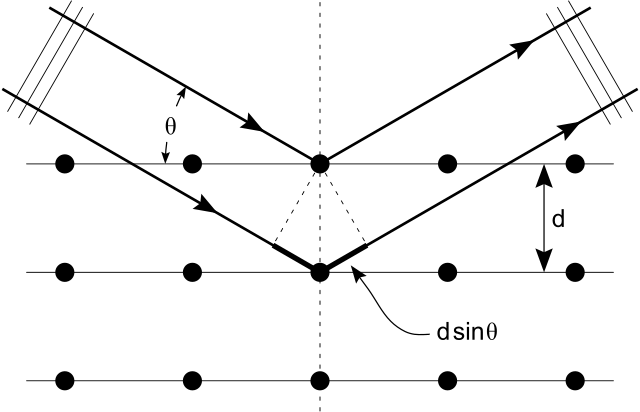
X-Ray Diffraction : Bragg’s Law of diffraction: illustration of how x-rays interact with crystal lattice.
Perhaps the most famous example of x-ray diffraction is the discovery of the double-helix structure of DNA in 1953. Using x-ray diffraction data, researchers were able to discern the structure of DNA shows a diffraction pattern produced by the scattering of x-rays from a crystal of protein. This process is known as x-ray crystallography because of the information it can yield about crystal structure. Not only do x-rays confirm the size and shape of atoms, they also give information on the atomic arrangements in materials. For example, current research in high-temperature superconductors involves complex materials whose lattice arrangements are crucial to obtaining a superconducting material. These can be studied using x-ray crystallography.

X-Ray Diffraction : X-ray diffraction from the crystal of a protein, hen egg lysozyme, produced this interference pattern. Analysis of the pattern yields information about the structure of the protein.
The Compton Effect
The Compton Effect is the phenomenon of the decrease in energy of photon when scattered by a free charged particle.
Objetivos de aprendizaje
Explain why Compton scattering is an inelastic scattering.
Puntos clave
Puntos clave
- Compton scattering is an example of inelastic scattering because the wavelength of the scattered light is different from the incident radiation.
- Like the photoelectric effects, the Compton effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Light must behave as if it consists of particles to explain the Compton scattering.
- Compton’s experiment convinced physicists that light can behave as a stream of particle-like objects (quanta) whose energy is proportional to the frequency.
Términos clave
- Doppler shift : is the change in frequency of a wave for an observer moving relative to its source.
- Thomson scattering : an elastic scattering of electromagnetic radiation by a free charged particle, as described by classical electromagnetism. It is just the low-energy limit of Compton scattering
- inelastic scattering : a fundamental scattering process in which the kinetic energy of an incident particle is not conserved
Compton scattering is an inelastic scattering of a photon by a free charged particle (usually an electron). It results in a decrease in energy (increase in wavelength) of the photon (which may be an X-ray or gamma ray photon), called the Compton Effect. Part of the energy of the photon is transferred to the scattering electron. Inverse Compton scattering also exists, and happens when a charged particle transfers part of its energy to a photon.
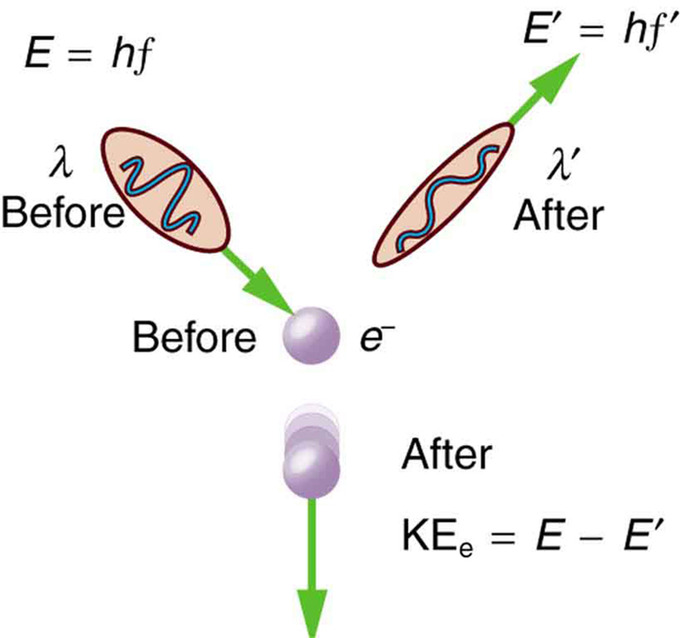
Scattering in the Compton Effect : The Compton Effect is the name given to the scattering of a photon by an electron. Energy and momentum are conserved, resulting in a reduction of both for the scattered photon. Studying this effect, Compton verified that photons have momentum.
Compton scattering is an example of inelastic scattering because the wavelength of the scattered light is different from the incident radiation. Still, the origin of the effect can be considered as an elastic collision between a photon and an electron. The amount of change in the wavelength is called the Compton shift. Although nuclear Compton scattering exists, Compton scattering usually refers to the interaction involving only the electrons of an atom.
The Compton effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Thomson scattering, the classical theory of an electromagnetic wave scattered by charged particles, cannot explain low intensity shifts in wavelength: classically, light of sufficient intensity for the electric field to accelerate a charged particle to a relativistic speed will cause radiation-pressure recoil and an associated Doppler shift of the scattered light. However, the effect will become arbitrarily small at sufficiently low light intensities regardless of wavelength. Light must behave as if it consists of particles to explain the low-intensity Compton scattering. Compton’s experiment convinced physicists that light can behave as a stream of particle-like objects (quanta) whose energy is proportional to the frequency.