Recordamos de Sección 5.14 , que, en un límite entre dos medios de permisos diferentes, el componente normal de ( textbf {D} ) y el componente tangencial de ( textbf { E} ) son continuos, mientras que el componente tangencial de ( textbf {D} ) es proporcional a ( epsilon ) y el componente normal de ( textbf {E} ) es inversamente proporcional a ( epsilon ). Las líneas de fuerza eléctrica se refractan en un límite de tal manera que
[ frac { tan theta_1} { tan theta_2} = frac { epsilon_1} { epsilon_2}. ]
La situación es similar con los campos magnéticos. Es decir, en un límite entre dos medios de permeabilidades diferentes, el componente normal de ( textbf {B} ) y el componente tangencial de ( textbf {H} ) son continuos, mientras que el componente tangencial de ( textbf {B} ) es proporcional a m y el componente normal de ( textbf {H} ) es inversamente proporcional a ( mu ) . Las líneas de fuerza magnética se refractan en un límite de tal manera que
[ frac { tan theta_1} { tan theta_2} = frac { mu_1} { mu_2}. ]
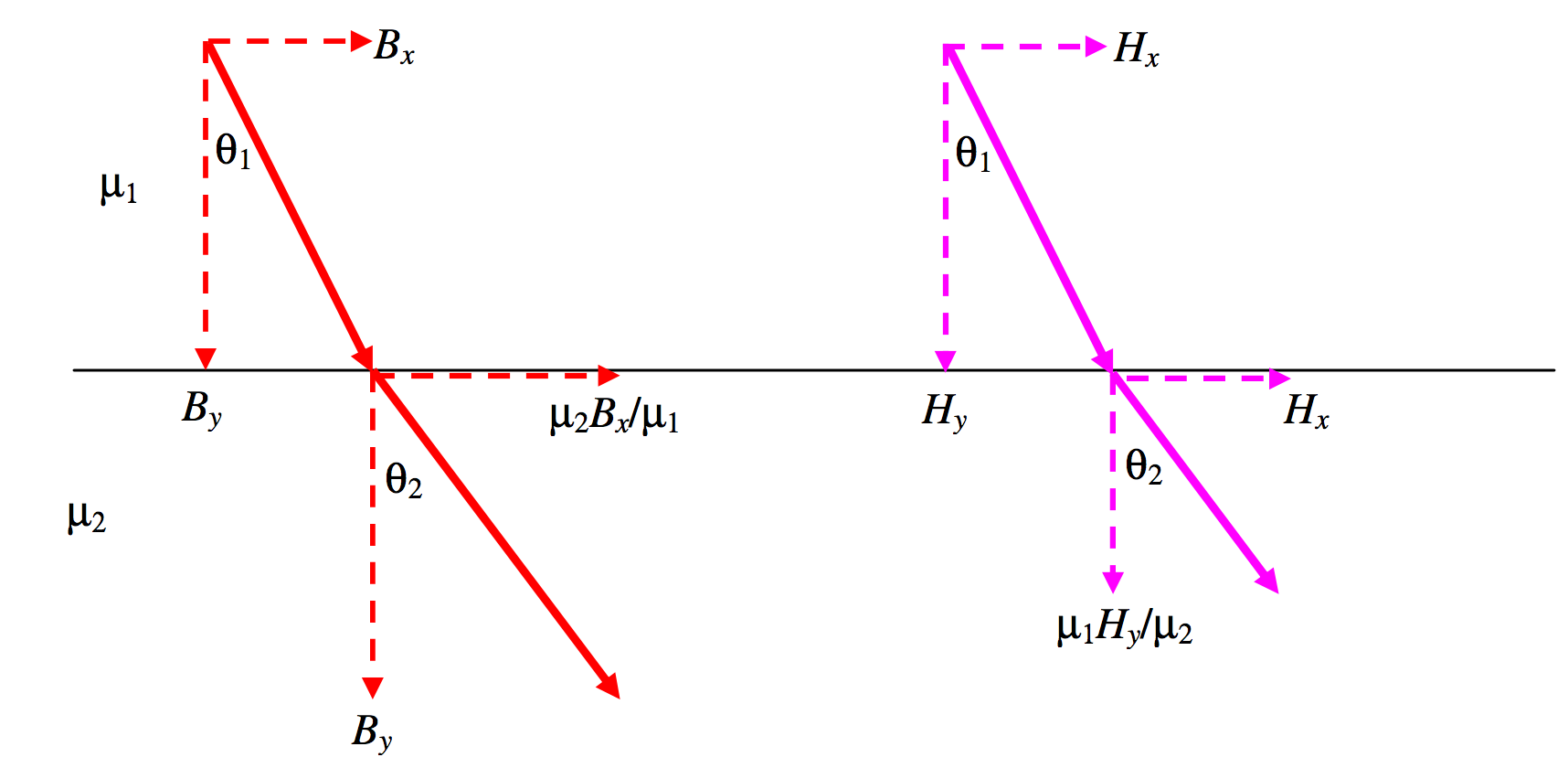
( text {FIGURA VI.16} )
La configuración del campo magnético dentro de un solenoide infinitamente largo con materiales de diferentes permeabilidades necesita un poco de cuidado. Nos guiaremos por la ley de Biot-Savart, a saber, (B = frac { mu I , ds , sin theta} {4 pi r} ), y la ley de Ampère, a saber, que la línea es integral de ( textbf {H} ) alrededor de un circuito cerrado es igual a la corriente encerrada. También recordamos que el campo magnético dentro de un solenoide infinito que contiene un único material isotrópico homogéneo es uniforme, es paralelo al eje del solenoide y está dado por (H = nI ) o (B = mu nI ) .
El caso de dos materiales más fácil de considerar es aquel en el que los dos materiales están dispuestos en paralelo como en la Figura VI.17.
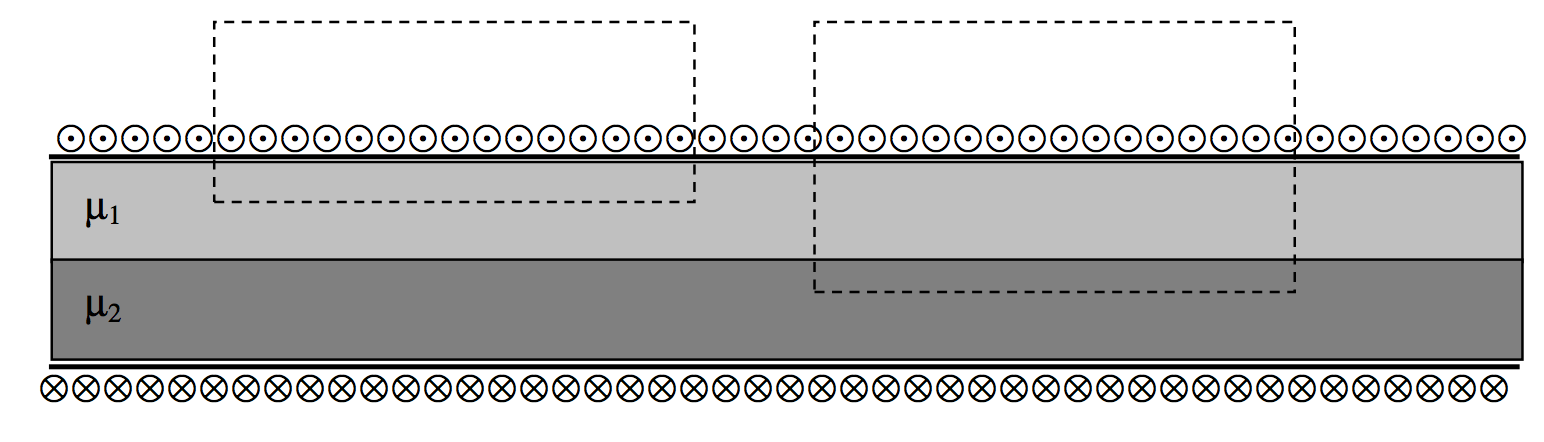
( text {FIGURA VI.17} )
Se puede ver aplicando la ley de Ampère a cada uno de los dos circuitos indicados por líneas discontinuas que el campo (H ) – es el mismo en cada material y es igual a (nI ), y es uniforme en todo el solenoide. Está dirigida paralela al eje del solenoide. Es decir, el componente tangencial de ( textbf {H} ) es continuo. Sin embargo, los campos (B ) en los dos materiales son diferentes, siendo ( mu_1 nI ) en el material superior y ( mu_2 nI ) en el inferior.
Ahora observamos la situación en la que los dos materiales están en serie, como en la Figura VI.18.
Usaremos una coordenada horizontal (x ), que es cero en el límite, negativa a la izquierda y positiva a la derecha.
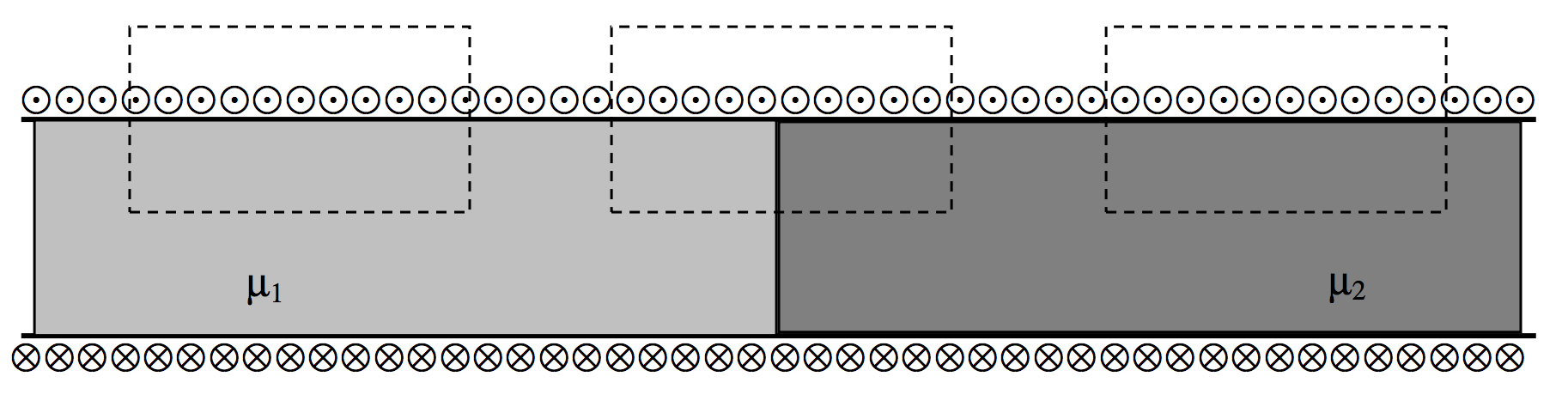
( text {FIGURA VI.18} )
Al principio podríamos sentir la tentación de suponer que (B = mu_1 nI ) a la izquierda del límite y (B = mu_2 nI ) a la derecha del límite, mientras que, mediante una aplicación de La ley de Ampère alrededor de cualquiera de los circuitos discontinuos indicados, (H = nI ) en ambos lados. Por tentador que sea, no es correcto, y veremos por qué en breve.
El campo (B ) – es de hecho ( mu_1 nI ) un largo camino hacia la izquierda del límite, y ( mu_2 nI ) un largo camino hacia la derecha. Sin embargo, cerca del límite está entre estos valores límite. Podemos calcular el campo (B ) en el eje en el límite por el mismo método que usamos en la Sección 6.8. Ver especialmente la ecuación 6.8, que, con la geometría actual, se convierte en
[B = frac {1} {2} mu_1 nI int _ {- pi / 2} ^ {0} cos theta , d theta + frac {1} {2} mu_2 nI int_ {0} ^ { pi / 2} cos theta , d theta. label {6.12.1} ]
No debería sorprender que esto llegue a
[B = frac {1} {2} ( mu_1 + mu_2) nI. Label {6.12.2} ]
Es lo mismo justo a la izquierda del límite y justo a la derecha.
El campo (H ), sin embargo, cae repentinamente en el límite desde ( frac {1} {2} left (1+ frac { mu_2} { mu_1} right) nI ) inmediatamente a la izquierda del límite a ( frac {1} {2} left (1+ frac { mu_1} { mu_2} right) nI ) inmediatamente a la derecha del límite.
En cualquier caso, los resultados muy importantes de estas consideraciones son
- En un límite entre dos medios de permeabilidades diferentes, el componente paralelo de ( textbf {H} ) es continuo, y el componente perpendicular de ( textbf {B} ) es continuo.
Compare y contraste esto con la caja eléctrica:
- En un límite entre dos medios de permisos diferentes, el componente paralelo de ( textbf {E} ) es continuo, y el componente perpendicular de ( textbf {D} ) es continuo.