Esta vez, la carga en el condensador está aumentando, por lo que la corriente, como se dibuja, es (+ dot Q ).
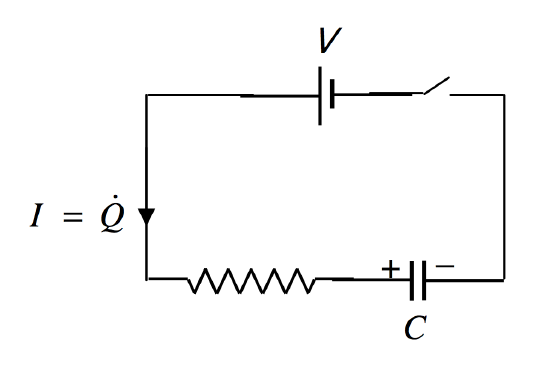
( text {FIGURE V.25} )
Así
[V- dot QR- frac {Q} {C} = 0 label {5.19.1} ]
De dónde:
[ int_0 ^ Q frac {dQ} {CV-Q} = frac {1} {RC} int_0 ^ t dt. Label {5.19.2} ]
Nota
No se sienta tentado a escribir la ecuación ( ref {5.19.2} ) como
[ int_0 ^ Q frac {dQ} {Q- CV} = – frac {1} {RC} int_0 ^ t dt. ]
Recuerde que, en cualquier finito (t ), (Q ) es menor que su valor asintótico (CV ), y desea mantener el denominador de la integral izquierda positivo.
Al integrar la ecuación ( ref {5.19.2} ), obtenemos
[Q = CV left (1-e ^ {- t / (RC)} derecha). label {5.19.3} ]
Por lo tanto, la carga en el condensador se aproxima asintóticamente a su valor final (CV ), alcanzando el 63% (1 – e – 1 ) del valor final en el tiempo (RC ) y la mitad del valor final en el tiempo (RC ln 2 = 0,6931 , RC )
La diferencia de potencial entre las placas aumenta a la misma velocidad. La diferencia de potencial no puede cambiar instantáneamente en ningún circuito que contenga capacitancia.
¿Cómo cambia la corriente con el tiempo? Esto se encuentra al diferenciar la Ecuación ref {5.19.3} con respecto al tiempo, para dar
[I = frac {V} {R} e ^ {- t / (RC)}. ]
Esto sugiere que la corriente crece instantáneamente de cero a (V / R ) tan pronto como se cierra el interruptor, y luego decae exponencialmente, con constante de tiempo (RC ), a cero. ¿Es esto realmente posible? En principio, es posible si la inductancia (ver Capítulo 12 ) del circuito es cero. Pero la inductancia de cualquier circuito cerrado no puede ser exactamente cero, y el circuito, como se dibuja sin ninguna inductancia, no se puede lograr en ningún circuito real, por lo que, en un circuito real, no habrá un cambio instantáneo de corriente. La sección 10.15 se ocupará del crecimiento de la corriente en un circuito que contiene capacitancia e inductancia, así como resistencia.
Cuando el capacitor está completamente cargado, la corriente ha caído a cero, la diferencia de potencial entre sus placas es (V ) (el EMF de la batería) y la energía almacenada en el condensador (consulte Sección 5.10 ) es
[ frac {1} {2} CV ^ 2 = frac {1} {2} QV. ]
Pero la energía perdida por la batería es (QV ). Esperemos que el ( frac {1} {2} QV ) restante sea calor generado y disipado por la resistencia. La tasa a la cual el calor es generado por la corriente en una resistencia (vea el Capítulo 4 Sección 4.6) es (I ^ 2R ). En este caso, de acuerdo con el párrafo anterior, la corriente en el momento (t ) es
[I = frac {V} {R} e ^ {- t / (RC)}, ]
por lo que el calor total generado en la resistencia es
[ frac {V ^ 2} {R} int_0 ^ { infty} e ^ {- 2t / (RC) } = frac {1} {2} CV ^ 2, ]
así que todo está bien. La energía perdida por la batería se comparte por igual entre (R ) y (C ) .
Lámpara de neón
Aquí hay una manera de hacer que una lámpara de neón parpadee periódicamente.
En la Figura (V. ) 25 ( frac {1} {2} ) (¡perdón por la fracción – introduje la Figura como una ocurrencia tardía!), La cosa que se parece a algo una cara feliz a la derecha es un tubo de descarga; el punto en su interior indica que no es un vacío completo en el interior, pero tiene un poco de gas en el interior.
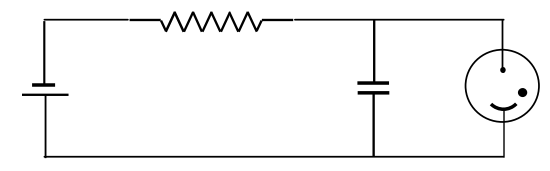
( text {FIGURE V.25} frac {1} {2} )
Se descargará cuando la diferencia de potencial a través del electrodos es más alto que un cierto umbral. Cuando se aplica un campo eléctrico a través del tubo, los electrones y los iones positivos se aceleran, pero pronto se reducen por colisiones. Pero, si el campo es suficientemente alto, los electrones e iones tendrán suficiente energía en la colisión para ionizar los átomos con los que colisionan, por lo que se producirá una descarga en cascada. La diferencia de potencial aumenta exponencialmente en una escala de tiempo (RC ) hasta que alcanza el valor umbral, y el tubo de neón se descarga repentinamente. Entonces empieza todo de nuevo.
Ejemplo ( PageIndex {1} )
Aquí hay un problema que dará práctica para cargar un condensador, aplicar las reglas de Kirchhoff y resolver ecuaciones diferenciales.
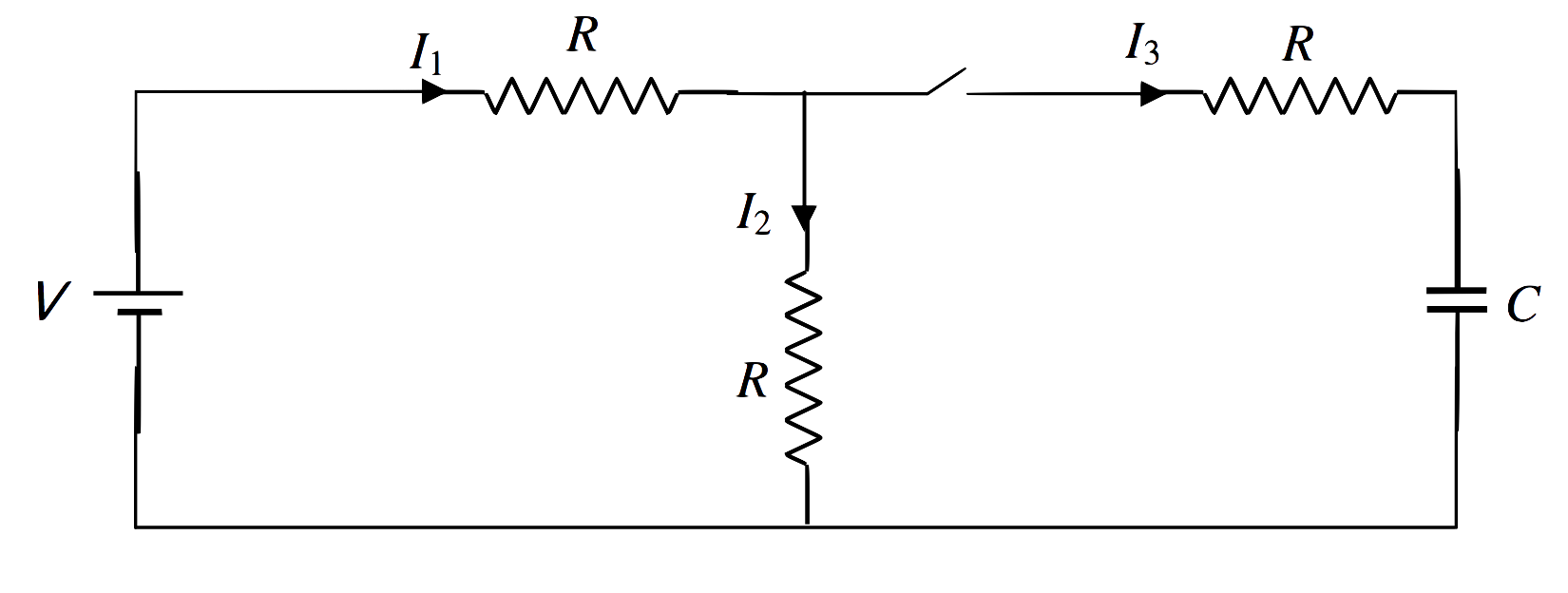
En el circuito anterior, mientras el interruptor está abierto, (I_1 = I_2 = V / (2R) ) y (I_3 = 0 ). Esta también será la situación mucho después de que se cierre el interruptor y se cargue el condensador. Pero queremos investigar qué sucede en los breves momentos mientras se carga el condensador. ¿Y cuál será la carga final en el condensador?
Aplicamos las reglas de Kirchhoff :
[V = I_1R + I_2R label {5.19.4} ]
[I_3R + Q / C-I_2R = 0 label {5.19.5} ]
[I_1 = I_2 + I_3, label {5.19.6} ]
Aquí (Q ) es la carga en el capacitor en algún momento.
Elimina (I_1 ) y (I_2 ) para obtener una sola ecuación en (I_3 ).
[V = frac {2Q} {C} + 3I_3R. Label {5.19.7} ]
Pero (I_3 = frac {dQ} {dt} ), entonces tenemos una ecuación diferencial en (Q ) y el tiempo (t ).
[ frac {dQ} {dt} + dfrac {2} {3RC} Q = frac {V} {3R}. Label {5.19.8} ]
[19459001 ] Esto es de la forma ( frac {dy} {dx} + ay = b ), y aquellos con experiencia en ecuaciones diferenciales no tendrán dificultad en llegar a la solución
[Q = frac {1} {2} CV + Ae ^ {- frac {2t} {3RC}} label {5.19.9} ]
Con la condición inicial de que (Q = 0 ) cuando (t = 0 ), esto se convierte en
[Q = frac {1} {2} CV left (1 -e ^ {- frac {2t} {3RC}} right). label {5.19.10} ]
Por lo tanto, la carga final en el condensador es ( frac {1} {2} CV ).
La corriente (I_3 ) se encuentra diferenciando la Ecuación ref {5.19.10} con respecto al tiempo, y las otras corrientes se encuentran en las reglas de Kirchhoff (Ecuaciones ref {5.19.4} – ref {5.19.6}). Los hago:
[I_1 = frac {V} {2R} left (1+ frac {1} {3} e ^ {- frac {2t} {3RC}} right ) label {5.19.11} ]
[I_2 = frac {V} {2R} left (1- frac {1} {3} e ^ {- frac {2t} {3RC}} right) label {5.19.12} ]
[I_3 = frac {V} {3R} e ^ {- frac {2t} {3RC}} label { 5.19.13} ]
Por lo tanto, (I_1 ) pasa de inicialmente ( frac {2V} {3R} ) a finalmente ( frac {V} {2R} ).
(I_2 ) va desde inicialmente ( frac {V} {3R} ) hasta finalmente ( frac {V} {2R} ).
(I_3 ) pasa de inicialmente ( frac {V} {3R} ) a finalmente 0.
Antes de abrir el interruptor, estas corrientes fueron ( frac {V} {2R} ), ( frac {V} {2R} ) y cero respectivamente. Los lectores pueden preguntarse si las corrientes pueden cambiar instantáneamente tan pronto como se cierra el interruptor . La respuesta es sí, siempre que el circuito no tenga inductancia (ver Capítulo 10 , especialmente las Secciones 10.12-15, que tratan del crecimiento de la corriente en un circuito que tiene inductancia). En la práctica, ningún circuito puede estar completamente libre de inductancia; Además de la inductancia de cualquier componente del circuito, cualquier circuito que forme un circuito cerrado (como todos los circuitos deben) debe tener una pequeña inductancia. La inductancia puede ser muy pequeña, lo que significa que el cambio de corriente en el instante en que se cierra el interruptor es muy rápido. Sin embargo, no es instantáneo.
Aquí hay gráficos de las corrientes y de (Q ) en función del tiempo. Las corrientes se expresan en unidades de (V / R ), (Q ) en unidades de (CV ) y el tiempo en unidades de ( frac {3} {2} RC ).
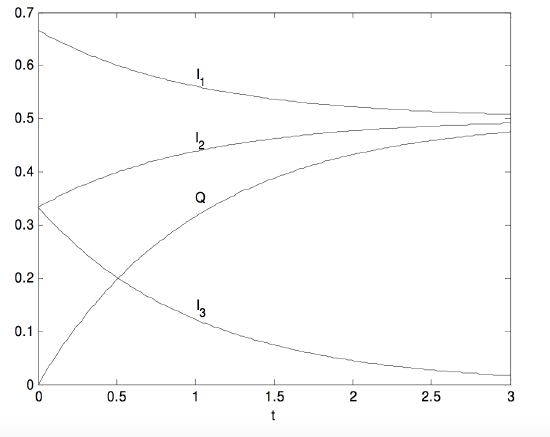
Hay un problema similar relacionado con un inductor en el Capítulo 10, Sección 10.12.
Veamos ahora qué sucede si conectamos una resistencia y un condensador en serie a través de una fuente de voltaje que varía con el tiempo, y lo demostraremos, siempre que se cumplan algunas condiciones , la diferencia de potencial a través del condensador es la integral de tiempo del voltaje de entrada, mientras que la diferencia de potencial a través de la resistencia es la derivada de tiempo del voltaje de entrada.
Hemos visto que, si conectamos una resistencia y un condensador en serie con una batería de EMF (V ), la carga en el condensador aumentará de acuerdo con
[Q = CV left (1-e ^ {- dfrac {t} {RC}} right) ]
y se acerca asintóticamente a (Q = CV ), y llega a (1-e ^ {-1} = 0.632 ) de este valor en el tiempo (RC ). Tenga en cuenta que, cuando (t << RC ), la corriente será grande y la carga en el condensador será pequeña. La mayor parte de la caída potencial en el circuito será a través de la resistencia, y relativamente poco a través del condensador. Sin embargo, después de mucho tiempo, la corriente será baja y la carga será alta, de modo que la mayor parte de la caída de potencial se realizará a través del condensador y relativamente poco a través de la resistencia. El potencial cae en R y C será igual a la vez
[t = RC ln 2 = 0.693RC. ]
[19459001 ] Suponga que, en lugar de conectar (R ) y (C ) a una batería de EMF constante, la conectamos a una fuente cuyo voltaje varía con el tiempo, (V (t) ). ¿Cómo variará el cargo en (C ) con el tiempo?
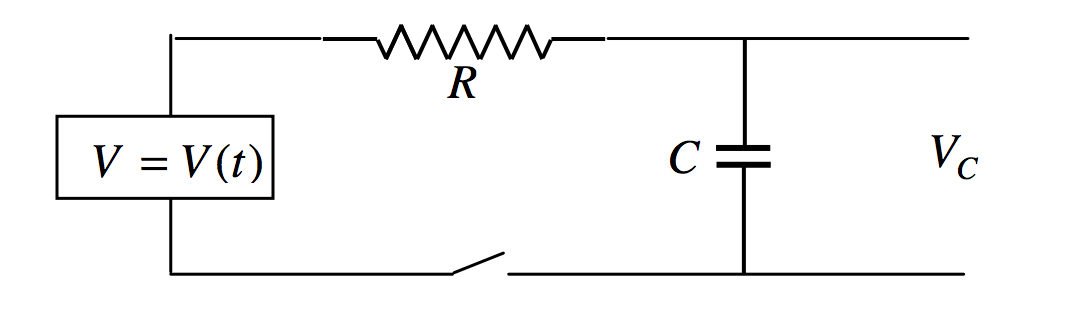
La ecuación relevante es (V = IR + Q / C ), en la que (I, , Q text {y} V ) son todos funciones del tiempo
Dado que (I = dot Q ), la ecuación diferencial que muestra cómo (Q ) varía con el tiempo es
[ dfrac {dQ} {dt} + dfrac {1} {RC} Q = dfrac {V} {R} label {5.19.14} ]
La integración de esta ecuación se facilita si multiplicamos ambos lados por (e ^ { dfrac {t} {RC}} ). (Los que tienen experiencia en la resolución de ecuaciones diferenciales pensarán fácilmente en este paso. Los que tienen menos experiencia podrían no pensar de inmediato en él, pero pronto verán que es un paso útil). Luego obtenemos
[e ^ { dfrac {t} {RC}} dfrac {dQ} {dt} + dfrac {1} {RC} e ^ { dfrac {t} {RC}} Q = dfrac {d} { dt} left (Qe ^ { dfrac {t} {RC}} right) = dfrac {V} {R} e ^ { dfrac {t} {RC}} label {5.19.15} ]
Por lo tanto, la respuesta a nuestra pregunta es
[Q = dfrac {e ^ {- dfrac {t} {RC}}} {R} int Ve ^ { dfrac {t} {RC}} , dt. label {5.19.16} ]
Si (V ) es independiente del tiempo, esto se reduce a la familiar (Q = CV left ( 1-e ^ {- dfrac {t} {RC}} right) ).
La diferencia de potencial entre (C ) aumenta, por supuesto, a medida que
[V_c = dfrac {e ^ {- dfrac {t} {RC}}} {RC } int Ve ^ { dfrac {t} {RC}} , dt. label {5.19.17} ]
Mientras que (t ) es mucho más corto que la constante de tiempo (RC ), con lo cual quiero decir lo suficientemente corto como para que (e ^ { dfrac {t} {RC}} ) esté muy cerca de 1, esto se convierte en
[V_c = dfrac {1} {RC} int V , dt label {5.19.18} ]
Eso es por qué este circuito se llama circuito integrador . El voltaje de salida a través de (C ) es (1 / (RC) ) veces la integral de tiempo del voltaje de entrada (V. ) Esto también es cierto si el voltaje de entrada es una función periódica del tiempo con un período que es mucho más corto que la constante de tiempo.
A modo de ejemplo, suponga que (V = at ^ 2 ) . Si ponemos esto en el lado derecho de la Ecuación ref {5.19.17} e integramos, con la condición inicial (V_C = 0 ) cuando (t = 0 ), (¡hazlo!), Obtenemos [19459009 ]
[V_c = aR ^ 2C ^ 2 left ( dfrac {t ^ 2} {R ^ 2C ^ 2} – dfrac {2t} {RC} + 2-2e ^ {- dfrac {t} {RC}} right). label {5.19.19} ]
Por ejemplo, suponga que el voltaje de entrada varía como (V = 5t ^ 2 ) voltios, donde (t ) está en segundos. Si (R = 500 Omega ) y (C = 400 mu text {F} ), ¿cuál será la diferencia de potencial a través del condensador después de 0.3 s? Inmediatamente vemos que (RC = 0.2 text {s} ) y (t / (RC) = 1.5 ). Sustituya los números SI en la ecuación ref {5.19.19} para obtener (V_C = 0.161 V. )
Si escribo (y = frac {V_c} {aR ^ 2C ^ 2} ) y (x = frac {t} {RC} ) La ecuación ref {5.19.19} en forma adimensional se convierte en
[y = x ^ 2-2x + 2-2e ^ {- x }. label {5.19.20} ]
Si Taylor expande esto hasta (x ^ 3 ) (¡hágalo!), obtiene (y = dfrac {1} { 3} x ^ 3 ), que es exactamente lo que obtendría al usar la ecuación ref {5.19.18}, la ecuación que es una aproximación para un tiempo corto en comparación con (RC ). La aproximación es buena siempre que ( left ( dfrac {t} {RC} right) ^ 4 ) sea insignificante. Muestro la ecuación ref {5.19.20} y (y = dfrac {1} {3} x ^ 3 ) en el gráfico a continuación, en el que (V_C ) está en unidades de (aR ^ 2C ^ 2 ) y (T ) está en unidades de (RC ).
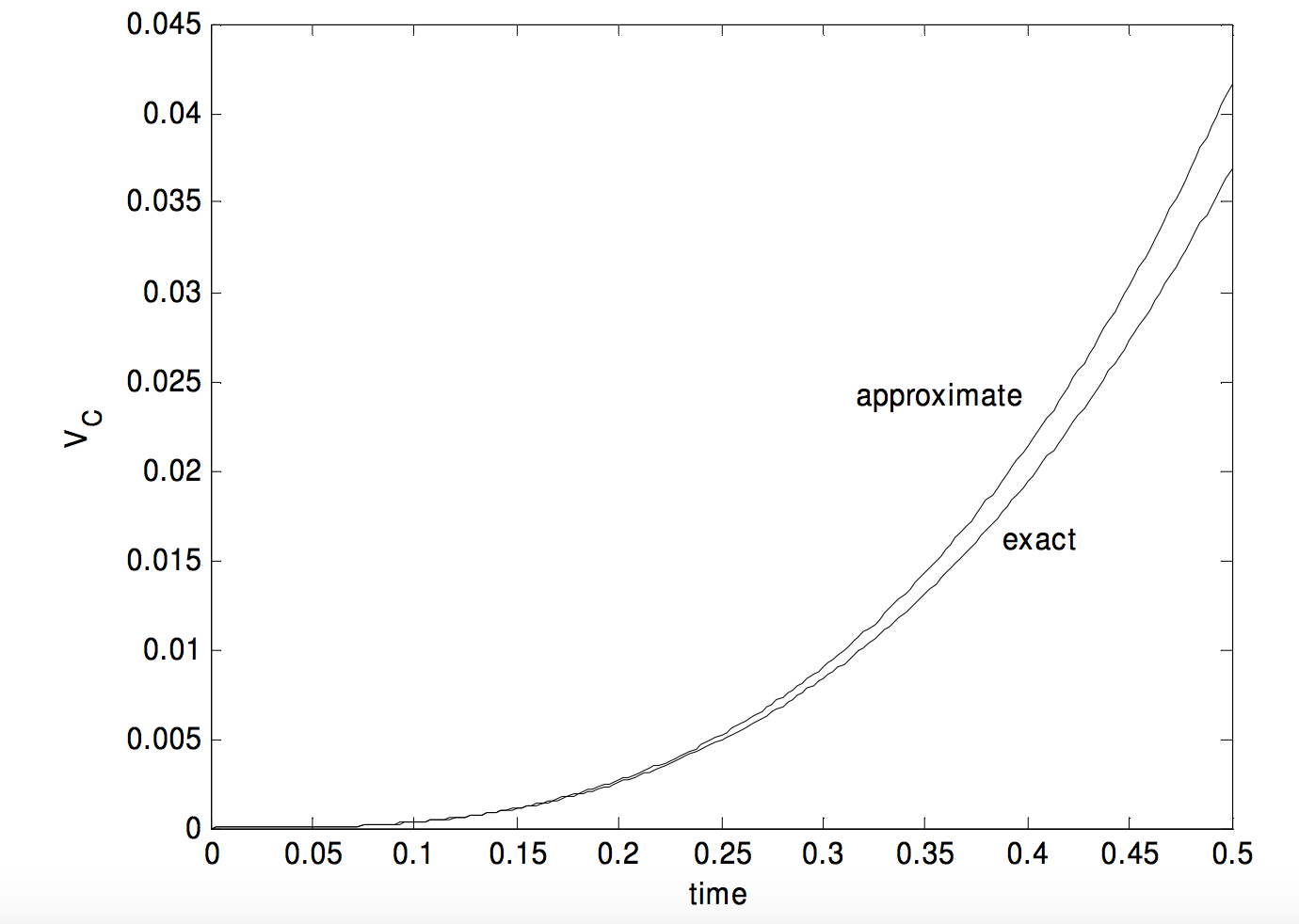
Ecuación ref {5.19.17} (o, para intervalos de tiempo cortos, la Ecuación ref {5.19.18}) nos da el voltaje a través de C [ 19459011] en función del tiempo. ¿Qué pasa con el voltaje a través de (R )? Eso es evidentemente
[V_R = V- dfrac {e ^ {- dfrac {t} {RC}}} {RC} int Ve ^ { dfrac {t} {RC}} , dt. label {5.19.21} ]
Diferenciar con respecto al tiempo:
[ begin {align} dfrac {dV_R} {dt} & = dfrac { dV} {dt} – dfrac {1} {RC} left (e ^ {- frac {t} {RC}} Ve ^ { dfrac {t} {RC}} – dfrac {e ^ {- dfrac {t} {RC}}} {RC} int Ve ^ { dfrac {t} {RC}} , dt right) \ & = dfrac {dV} {dt} – dfrac {1 } {RC} (V-V_C) = dfrac {dV} {dt} – dfrac {V_R} {RC} \ end {align} label {5.19.22} ]
Si la constante de tiempo es pequeña, de modo que ( dfrac {dV_R} {dt} ll < dfrac {V_R} {RC} ), esto se convierte en
[V_R = RC dfrac {dV} { dR}, label {5.20.23} ]
para que el voltaje a través de (R ) sea (RC ) multiplicado por la derivada de tiempo del voltaje de entrada (V. ) Así tener un circuito diferenciador.
Tenga en cuenta que, en el circuito que integra , el circuito debe tener una constante de tiempo grande (grande (R ) y (C ) ) y las variaciones de tiempo en (V ) son rápidas en comparación con (RC ). El voltaje de salida a través de (C ) es entonces ( dfrac {1} {RC} int V , dt ). En el circuito diferenciador , el circuito debe tener una pequeña constante , y las variaciones de tiempo en (V ) son lentas comparadas con (RC ). El voltaje de salida a través de (R ) es entonces ( dfrac {dV} {dR} ).