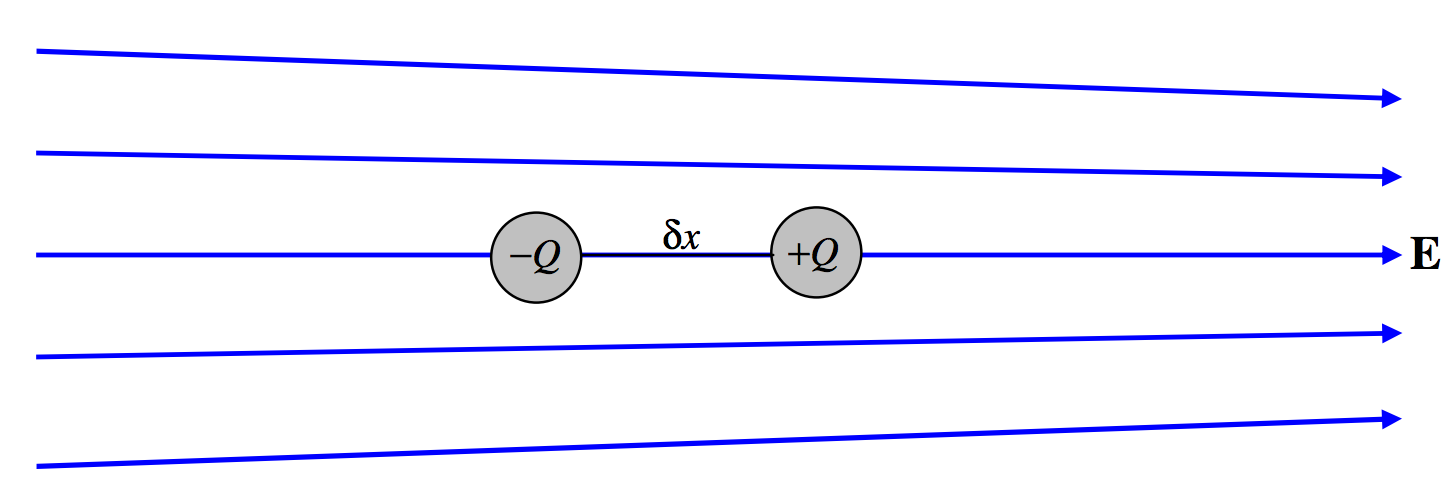
Considere un dipolo simple que consta de dos cargas (+ Q ) y (- Q ) separadas por una distancia (δx ), de modo que su momento dipolar es (p = Q , δx ). Imagine que está situado en un campo eléctrico no homogéneo como se muestra en la Figura (III ). 4. Ya hemos notado que un dipolo en un campo homogéneo no experimenta fuerza neta, pero podemos ver que sí experimenta una fuerza neta en un campo no homogéneo . Deje el campo en (- Q text {be} E ) y el campo en (+ Q text {be} E + δE ). La fuerza sobre (- Q text {es} QE ) a la izquierda, y la fuerza sobre (+ Q text {es} Q (E + δE) ) a la derecha. Por lo tanto, hay una fuerza neta a la derecha de (Q , δE ), o:
[ label {3.5.1} text {Force} = p frac {dE} {dx } ]
La ecuación ref {3.5.1} describe la situación en la que el dipolo, el campo eléctrico y el gradiente son todos paralelos al eje x . En una situación más general, los tres están en direcciones diferentes. Recordemos que el campo eléctrico es menos gradiente potencial. El potencial es una función escalar, mientras que el campo eléctrico es una función vectorial con tres componentes, de los cuales el componente x , por ejemplo, es (E_x = – frac {∂V} {∂x} ) . El gradiente de campo es un tensor simétrico que tiene nueve componentes (de los cuales, sin embargo, solo seis son distintos), como ( frac {∂ ^ 2V} {∂x ^ 2}, , frac { ∂ ^ 2V} {∂y ∂z} ) etc. Así, en general, la ecuación ref {3.5.1} debería escribirse como
[ begin {pmatrix} E_x \ E_y \ E_z \ end {pmatrix} = – begin {pmatrix} V_ {xx} & V_ {xy} & V_ {xz} \ V_ {xy} & V_ {yy} & V_ {yz} \ V_ {xz } & V_ {yz} & V_ {zz} \ end {pmatrix} begin {pmatrix} p_x \ p_y \ p_z \ end {pmatrix} label {3.5.2} ]
[ 19459028] en el que los subíndices dobles en el tensor de gradiente potencial denotan las segundas derivadas parciales.