Considere un dipolo que oscila en un campo eléctrico (Figura III.3). Cuando está en un ángulo ( theta ) con respecto al campo, la magnitud del par de restauración es (pE sin theta ) y, por lo tanto, su ecuación de movimiento es
[I ddot theta = -pE sin theta label {1} ]
donde (I ) es su inercia rotacional.
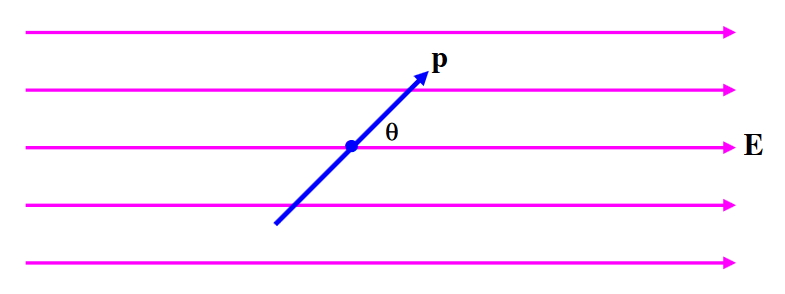
( text {FIGURA III.3} )
Para ángulos pequeños, la ecuación ( ref {1} ) puede aproximarse como
[I ddot theta approx -pE theta ]
y entonces el período de pequeñas oscilaciones es
[ label {3.3.1} P = 2 pi sqrt { frac {I} {pE}}. ]
¿Esperaría que el período fuera largo si la inercia rotacional fuera grande? ¿Esperaría que las vibraciones fueran rápidas si (p text {y} E ) fueran grandes? ¿Es la expresión anterior dimensionalmente correcta?