Habilidades para desarrollar
- Para saber cómo usar las vidas medias para describir las tasas de reacciones de primer orden
Otro enfoque para describir las velocidades de reacción se basa en el tiempo requerido para que la concentración de un reactivo disminuya a la mitad de su valor inicial. Este período de tiempo se denomina semivida de la reacción, escrita como t 1 / 2 . Así, la vida media de una reacción es el tiempo requerido para que la concentración del reactivo disminuya de [A] 0 a [A] 0/2 . Si dos reacciones tienen el mismo orden, la reacción más rápida tendrá una vida media más corta y la reacción más lenta tendrá una vida media más larga.
La vida media de una reacción de primer orden bajo un conjunto dado de condiciones de reacción es una constante. Esto no es cierto para las reacciones de cero y segundo orden. La vida media de una reacción de primer orden es independiente de la concentración de los reactivos. Esto se hace evidente cuando reorganizamos la ley de velocidad integrada para una reacción de primer orden (Ecuación 14.21) para producir la siguiente ecuación:
[ ln dfrac {[ textrm A] _0} {[ textrm A]} = kt label {21.4.1} ]
Sustituyendo [A] 0/2 por [A] y t 1 / 2 por t ] (para indicar una vida media) en La ecuación ( ref {21.4.1} ) da
[ ln dfrac {[ textrm A] _0} {[ textrm A] _0 / 2} = ln 2 = kt_ {1/2} ]
Sustituyendo ( ln {2} approx 0.693 ) en la ecuación, se obtiene la expresión de la vida media de una reacción de primer orden:
[t_ {1/2} = dfrac {0.693} {k} label {21.4.2} ]
Por lo tanto, para una reacción de primer orden, cada vida media sucesiva es el mismo período de tiempo, como se muestra en Figura ( PageIndex {1} ) , y es independiente de [A].
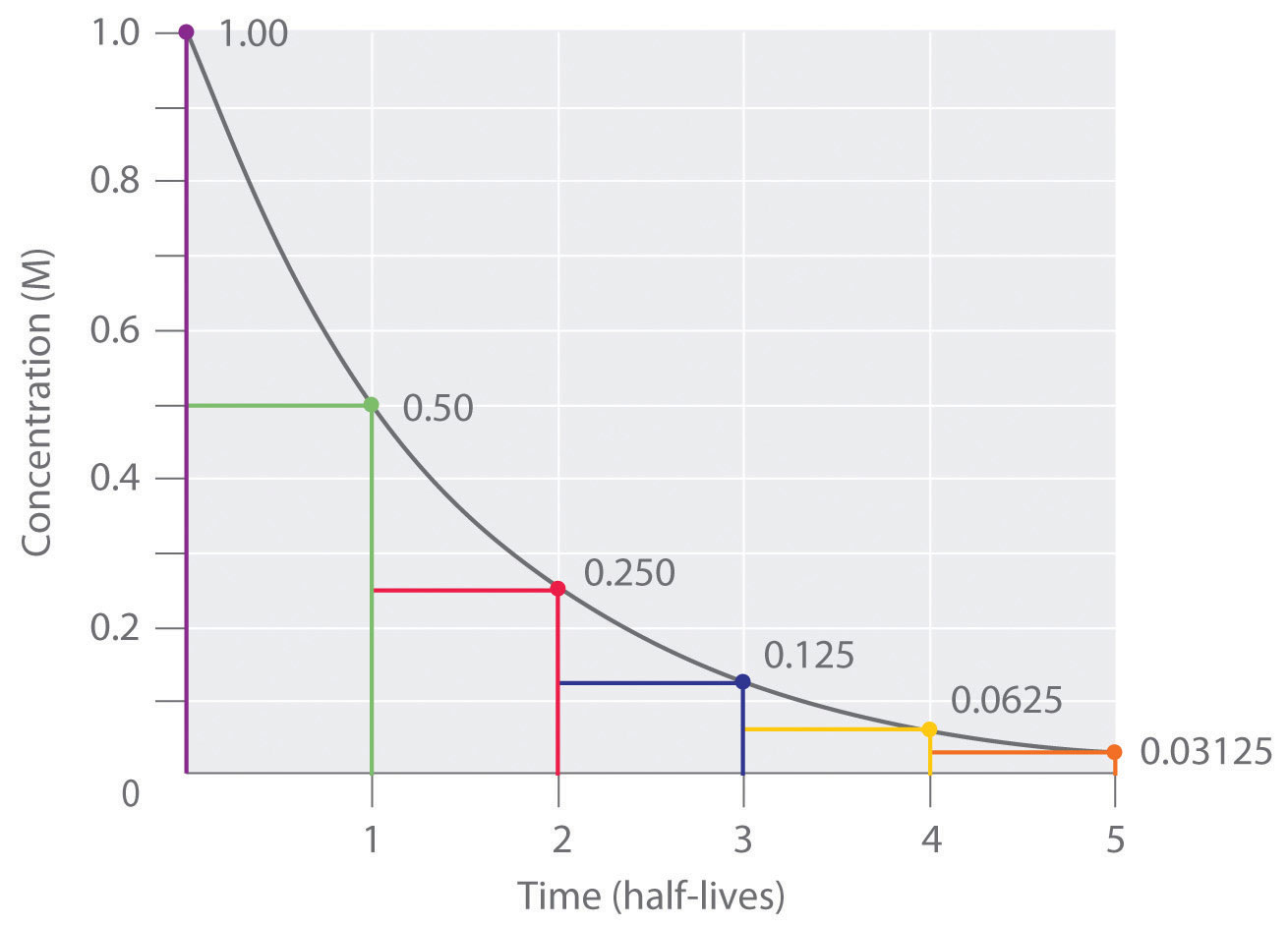
Si conocemos la constante de velocidad para una reacción de primer orden, entonces podemos usar vidas medias para predecir cuánto tiempo se necesita para que la reacción alcance un cierto porcentaje de finalización.
| Número de vidas medias | Porcentaje de reactivo restante | |
|---|---|---|
| 1 | ( dfrac {100 %} {2} = 50 % ) | ( dfrac {1} {2} (100 %) = 50 % ) |
| 2 | ( dfrac {50 %} {2} = 25 % ) | ( dfrac {1} {2} left ( dfrac {1} {2} right) (100 %) = 25 % ) |
| 3 | ( dfrac {25 %} {2} = 12.5 % ) | ( dfrac {1} {2} left ( dfrac {1} {2} right) left ( dfrac {1} {2} right) (100 %) = 12.5 % ) |
| n | ( dfrac {100 %} {2 ^ n} ) | ( left ( dfrac {1} {2} right) ^ n (100 %) = left ( dfrac {1} {2} right) ^ n % ) |
Como puede ver en esta tabla, la cantidad de reactivo que queda después de n semividas de una reacción de primer orden es (1/2) n [ 19459044] veces la concentración inicial.
Para una reacción de primer orden, la concentración del reactivo disminuye en una constante con cada vida media y es independiente de [A].
Ejemplo ( PageIndex {1} )
El fármaco anticancerígeno cis-platino se hidroliza en agua con una tasa constante de 1.5 × 10 −3 min −1 a pH 7.0 y 25 ° C. Calcule la vida media de la reacción de hidrólisis en estas condiciones. Si una solución recién preparada de cisplatino tiene una concentración de 0.053 M, ¿cuál será la concentración de cisplatino después de 5 semividas? después de 10 vidas medias? ¿Cuál es el porcentaje de finalización de la reacción después de 5 vidas medias? después de 10 vidas medias?
Dado: tasa constante, concentración inicial y número de semividas
Preguntado por: vida media, concentraciones finales y porcentaje de finalización
Estrategia:
- Use Ecuación ( ref {21.4.2} ) para calcular la vida media de la reacción.
- Multiplique la concentración inicial por 1/2 a la potencia correspondiente al número de semividas para obtener las concentraciones restantes después de esas semividas.
- Reste la concentración restante de la concentración inicial. Luego divida por la concentración inicial, multiplicando la fracción por 100 para obtener el porcentaje de finalización.
SOLUCIÓN
A Podemos calcular la vida media de la reacción usando Ecuación ( ref {21.4.2} ) :
(t_ {1/2} = dfrac {0.693} {k} = dfrac {0.693} {1.5 times10 ^ {- 3} textrm {min} ^ {- 1}} = 4.6 times10 ^ 2 textrm {min} )
Por lo tanto, tarda casi 8 h para que la mitad del cisplatino se hidrolice.
B Después de 5 vidas medias (aproximadamente 38 h), la concentración restante de cisplatino será la siguiente:
( dfrac {0.053 textrm {M}} {2 ^ 5} = dfrac {0.053 textrm {M}} {32} = 0.0017 textrm {M} )
Después de 10 vidas medias (77 h), la concentración restante de cisplatino será la siguiente:
( dfrac {0.053 textrm {M}} {2 ^ {10}} = dfrac {0.053 textrm {M}} {1024} = 5.2 times10 ^ {- 5} textrm {M} )
C El porcentaje de finalización después de 5 vidas medias será el siguiente:
( textrm {porcentaje de finalización} = dfrac {(0.053 textrm {M} -0.0017 textrm {M}) (100)} {0.053} = 97 % )
El porcentaje de finalización después de 10 vidas medias será el siguiente:
( textrm {porcentaje de finalización} = dfrac {(0.053 textrm {M} -5.2 times10 ^ {- 5} textrm {M}) (100)} {0.053 textrm {M}} = 100 % )
Por lo tanto, una reacción química de primer orden se completa al 97% después de 5 semividas y al 100% después de 10 semividas.
Ejercicio ( PageIndex {1} )
El cloruro de etilo se descompone en etileno y HCl en una reacción de primer orden que tiene una velocidad constante de 1.6 × 10 −6 s −1 a 650 ° C.
- ¿Cuál es la vida media de la reacción en estas condiciones?
- Si un matraz que originalmente contiene cloruro de etilo 0.077 M se calienta a 650 ° C, ¿cuál es la concentración de cloruro de etilo después de 4 vidas medias?
- Responda a
-
4,3 × 10 5 s = 120 h = 5,0 días;
- Respuesta b
-
4,8 × 10 −3 M
Tasas de descomposición radiactiva
La radiactividad, o desintegración radiactiva, es la emisión de una partícula o un fotón que resulta de la descomposición espontánea del núcleo inestable de un átomo. La tasa de desintegración radiactiva es una propiedad intrínseca de cada isótopo radiactivo que es independiente de la forma química y física del isótopo radiactivo. La tasa también es independiente de la temperatura. En esta sección, describiremos las tasas de desintegración radiactiva y cómo se pueden usar las vidas medias para monitorear los procesos de desintegración radiactiva.
En cualquier muestra de una sustancia radiactiva dada, el número de átomos del isótopo radiactivo debe disminuir con el tiempo a medida que sus núcleos se descomponen en núcleos de un isótopo más estable. Usando N para representar el número de átomos del isótopo radiactivo, podemos definir la tasa de descomposición de la muestra, que también se llama su actividad ( A ) como la disminución en el número de núcleos de radioisótopos por unidad de tiempo:
[A = – dfrac { Delta N} { Delta t} label {21.4.3} ]
La actividad generalmente se mide en desintegraciones por segundo (dps) o desintegraciones por minuto (dpm).
La actividad de una muestra es directamente proporcional al número de átomos del isótopo radiactivo en la muestra:
[A = kN label {21.4.4} ]
Aquí, el símbolo k es la constante de desintegración radiactiva, que tiene unidades de tiempo inverso (p. Ej., S −1 , año −1 ) y Un valor característico para cada isótopo radiactivo. Si combinamos Ecuación ( ref {21.4.3} ) y Ecuación ( ref {21.4.4} ) , obtenemos la relación entre el número de desintegraciones por unidad de tiempo y el número de átomos del isótopo en una muestra:
[- dfrac { Delta N} { Delta t} = kN label {21.4.5} ]
La ecuación ( ref {21.4.5} ) es la misma que la ecuación para la velocidad de reacción de una reacción de primer orden, excepto que usa números de átomos en lugar de concentraciones. De hecho, la desintegración radiactiva es un proceso de primer orden y puede describirse en términos de la ley de tasa diferencial ( Ecuación ( ref {21.4.5} ) ) o la ley de tasa integrada: [ 19459003]
[N = N_0e ^ {- kt} ]
[ ln dfrac {N} {N_0} = – kt label {21.4.6} ]
Debido a que la desintegración radiactiva es un proceso de primer orden, el tiempo requerido para que la mitad de los núcleos en cualquier muestra de un isótopo radiactivo decaiga es una constante, llamada semivida del isótopo. La vida media nos dice cuán radiactivo es un isótopo (el número de desintegraciones por unidad de tiempo); Por lo tanto, es la propiedad más comúnmente citada de cualquier radioisótopo. Para un número dado de átomos, los isótopos con vidas medias más cortas se descomponen más rápidamente, experimentando un mayor número de desintegraciones radiactivas por unidad de tiempo que los isótopos con vidas medias más largas. Las vidas medias de varios isótopos se enumeran en Tabla 14.6 , junto con algunas de sus aplicaciones.
| Isótopo radiactivo | Half-Life | Usos típicos |
|---|---|---|
| * El m denota metaestable, donde un núcleo en estado excitado se desintegra al estado fundamental del mismo isótopo. | ||
| hidrógeno-3 (tritio) | 12,32 años | marcador bioquímico |
| carbono-11 | 20,33 min | tomografía por emisión de positrones (imágenes biomédicas) |
| carbono-14 | 5,70 × 10 3 año | datación de artefactos |
| sodio-24 | 14,951 h | trazador del sistema cardiovascular |
| fósforo-32 | 14,26 días | marcador bioquímico |
| potasio-40 | 1.248 × 10 9 año | datación de rocas |
| hierro-59 | 44.495 días | marcador de vida de glóbulos rojos |
| cobalto-60 | 5.2712 años | radioterapia para el cáncer |
| tecnecio-99 m * | 6,006 h | imágenes biomédicas |
| yodo-131 | 8.0207 días | marcador de estudios de tiroides |
| radio-226 | 1.600 × 10 3 año | radioterapia para el cáncer |
| uranio-238 | 4.468 × 10 9 año | datación de rocas y corteza terrestre |
| americio-241 | 432,2 años | detectores de humo |
Nota
La desintegración radiactiva es un proceso de primer orden.
Técnicas de datación por radioisótopos
En nuestra discusión anterior, utilizamos la vida media de una reacción de primer orden para calcular cuánto tiempo había estado ocurriendo la reacción. Debido a que las reacciones de desintegración nuclear siguen una cinética de primer orden y tienen una velocidad constante que es independiente de la temperatura y el entorno químico o físico, podemos realizar cálculos similares utilizando la vida media de los isótopos para estimar las edades de los artefactos geológicos y arqueológicos. Las técnicas que se han desarrollado para esta aplicación se conocen como técnicas de datación por radioisótopos.
El método más común para medir la edad de los objetos antiguos es la datación por carbono 14. El isótopo de carbono 14, creado continuamente en las regiones superiores de la atmósfera de la Tierra, reacciona con el oxígeno u ozono atmosférico para formar 14 CO 2 . Como resultado, el CO 2 que las plantas usan como fuente de carbono para sintetizar compuestos orgánicos siempre incluye una cierta proporción de moléculas 14 CO 2 y no radiactivas 12 CO 2 y 13 CO 2 . Cualquier animal que come una planta ingiere una mezcla de compuestos orgánicos que contiene aproximadamente las mismas proporciones de isótopos de carbono que los de la atmósfera. Cuando el animal o la planta muere, los núcleos de carbono 14 en sus tejidos se descomponen en núcleos de nitrógeno 14 por un proceso radiactivo conocido como desintegración beta, que libera electrones de baja energía (partículas β) que pueden detectarse y medirse:
[ ce {^ {14} C rightarrow ^ {14} N + beta ^ {-}} label {21.4.7} ]
La vida media de esta reacción es de 5700 ± 30 años.
La relación 14 C / 12 C en organismos vivos es 1.3 × 10 −12 , con una tasa de descomposición de 15 dpm / g de carbono Figura ( PageIndex {2} ) ). Al comparar las desintegraciones por minuto por gramo de carbono de una muestra arqueológica con las de una muestra viva reciente, los científicos pueden estimar la edad del artefacto, como se ilustra en el Ejemplo 11. El uso de este método supone implícitamente que 14 CO 2 / 12 La relación CO 2 en la atmósfera es constante, lo cual no es estrictamente correcto. Se han utilizado otros métodos, como la datación de anillos de árbol, para calibrar las fechas obtenidas por datación por radiocarbono, y todas las fechas de radiocarbono informadas ahora se corrigen por cambios menores en 14 CO 2 / 12 CO 2 relación con el tiempo.
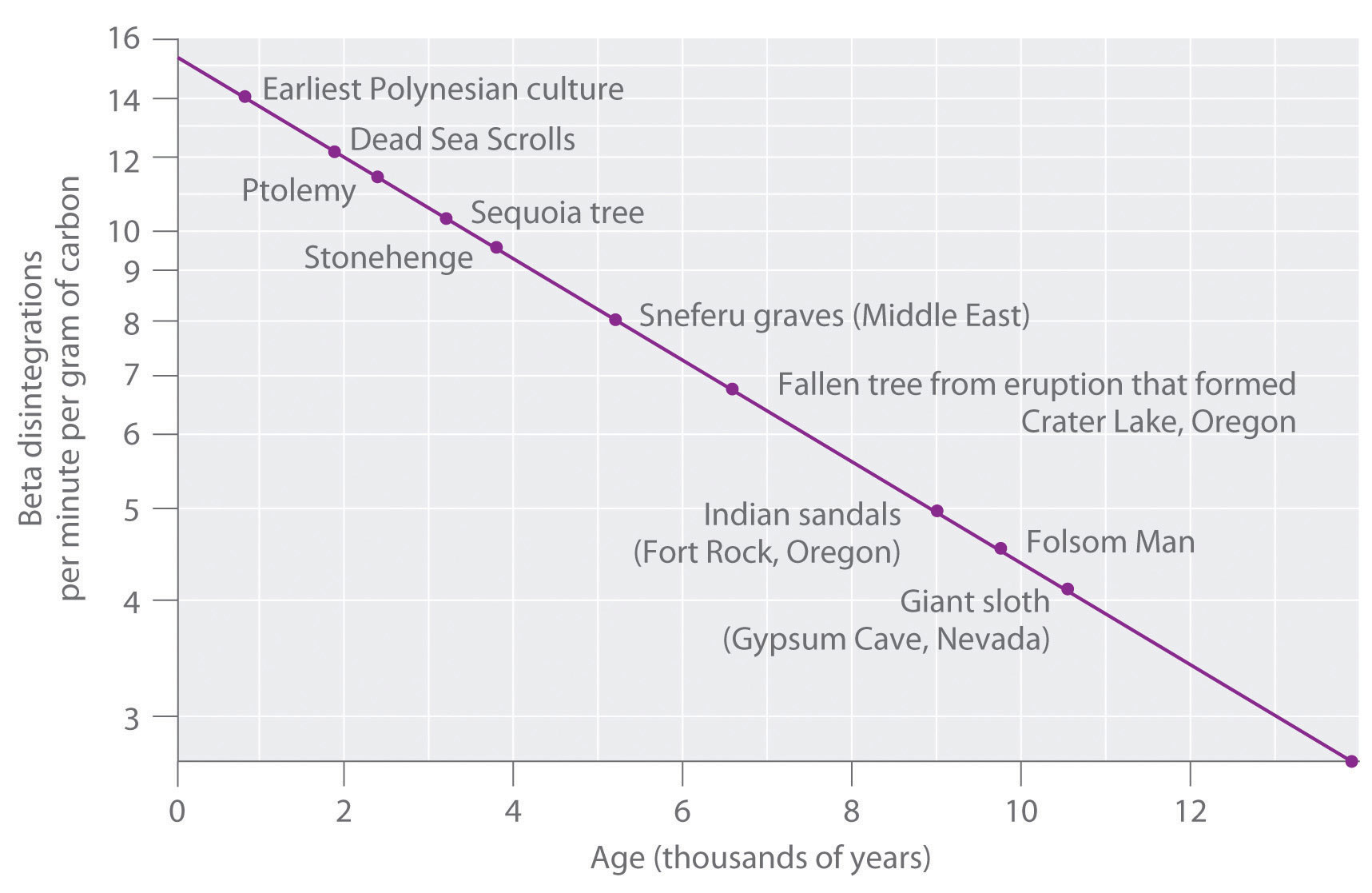
Ejemplo ( PageIndex {2} )
En 1990, los restos de un hombre aparentemente prehistórico fueron encontrados en un glaciar derritiéndose en los Alpes italianos. El análisis del contenido de 14 C de las muestras de madera de sus herramientas dio una tasa de descomposición de 8.0 dpm / g de carbono. ¿Hace cuánto tiempo murió el hombre?
Dado: isótopo y actividad final
Preguntado por: tiempo transcurrido
Estrategia:
A Use Ecuación ( ref {21.4.4} ) para calcular N 0 / N . Luego, sustituya el valor de la vida media de 14 C en Ecuación ( ref {21.4.2} ) para encontrar la velocidad constante de la reacción.
B Usando los valores obtenidos para N 0 / N y la constante de velocidad, resuelva Ecuación ( ref {21.4.6} ) para obtener el tiempo transcurrido.
SOLUCIÓN
Conocemos la actividad inicial de la identidad del isótopo (15 dpm / g), la actividad final (8.0 dpm / g) y la vida media, por lo que podemos usar la ley de velocidad integrada para una reacción nuclear de primer orden ( Ecuación ( ref {21.4.6} ) ) para calcular el tiempo transcurrido (la cantidad de tiempo transcurrido desde que se cortó la madera para las herramientas y comenzó a descomponerse).
( begin {align} ln dfrac {N} {N_0} & = – kt
\ dfrac { ln (N / N_0)} {k} & = t end {align } )
A De Ecuación ( ref {21.4.4} ) , sabemos que A = kN . Por lo tanto, podemos usar las actividades iniciales y finales ( A 0 = 15 dpm y A = 8.0 dpm) para calcular N [19459014 ] 0 / N :
( dfrac {A_0} {A} = dfrac {kN_0} {kN} = dfrac {N_0} {N} = dfrac {15} {8.0} )
Ahora solo necesitamos calcular la constante de velocidad para la reacción a partir de su vida media (5730 años) usando Ecuación ( ref {21.4.2} ) :
(t_ {1/2} = dfrac {0.693} {k} )
Esta ecuación se puede reorganizar de la siguiente manera:
(k = dfrac {0.693} {t_ {1/2}} = dfrac {0.693} {5730 textrm {año}} = 1.22 veces10 ^ {- 4} textrm {año} ^ { -1} )
B Sustituyendo en la ecuación t ,
(t = dfrac { ln (N_0 / N)} {k} = dfrac { ln (15 / 8.0)} {1.22 times10 ^ {- 4} textrm {año} ^ {- 1}} = 5.2 times10 ^ 3 textrm {año} )
Según nuestros cálculos, el hombre murió hace 5200 años.
Ejercicio ( PageIndex {2} )
Se cree que los humanos llegaron por primera vez al hemisferio occidental durante la última Edad de Hielo, presumiblemente viajando por un puente terrestre expuesto entre Siberia y Alaska. Los arqueólogos han estimado que esto ocurrió hace aproximadamente 11,000 años, pero algunos argumentan que los descubrimientos recientes en varios sitios en América del Norte y del Sur sugieren una llegada mucho más temprana. El análisis de una muestra de carbón de un incendio en uno de esos sitios proporcionó una velocidad de descomposición de 14 C de 0,4 dpm / g de carbono. ¿Cuál es la edad aproximada de la muestra?
- Respuesta
-
30,000 años
Resumen
- La vida media de una reacción de primer orden es independiente de la concentración de los reactivos.
- La vida media de los isótopos radiactivos se puede usar para fechar objetos.
La vida media de una reacción es el tiempo requerido para que la concentración de reactivo disminuya a la mitad de su valor inicial. La vida media de una reacción de primer orden es una constante relacionada con la constante de velocidad de la reacción: t 1 / 2 = 0,693 / k . Las reacciones de desintegración radiactiva son reacciones de primer orden. La tasa de descomposición, o actividad, de una muestra de una sustancia radiactiva es la disminución en el número de núcleos radiactivos por unidad de tiempo.