La magnitud de la constante de equilibrio para una reacción de ionización se puede usar para determinar las fuerzas relativas de ácidos y bases. Por ejemplo, la ecuación general para la ionización de un ácido débil en agua, donde HA es el ácido original y A− es su base conjugada, es la siguiente:
[HA _ {(aq)} + H_2O _ {(l)} rightleftharpoons H_3O ^ + _ {(aq)} + A ^ −_ {(aq)} label {16.5.1} ] [19459010 ]
La constante de equilibrio para esta disociación es la siguiente:
[K = dfrac {[H_3O ^ +] [A ^ -]} {[H_2O] [HA]} label {16.5.2} ]
Como notamos anteriormente, la concentración de agua es esencialmente constante para todas las reacciones en solución acuosa, por lo que ([H_2O] ) en la ecuación ( ref {16.5.2} ) puede incorporarse en una nueva cantidad , la constante de ionización ácida ( (K_a )), también llamada constante de disociación ácida:
[K_a = K [H_2O] = dfrac {[H_3O ^ +] [A ^ -]} {[HA]} label {16.5.3} ]
Por lo tanto, los valores numéricos de K y (K_a ) difieren según la concentración de agua (55,3 M). Nuevamente, por simplicidad, (H_3O ^ + ) se puede escribir como (H ^ + ) en la ecuación ( ref {16.5.3} ). Sin embargo, tenga en cuenta que no existe (H ^ + ) libre en soluciones acuosas y que se transfiere un protón a (H_2O ) en todas las reacciones de ionización ácida para formar iones hidronio, (H_3O ^ + ) . Cuanto mayor es (K_a ), más fuerte es el ácido y mayor es la concentración de (H ^ + ) en equilibrio. Como todas las constantes de equilibrio, las constantes de ionización ácido-base se miden en términos de las actividades de (H ^ + ) u (OH ^ – ), lo que las hace sin unidades. Los valores de (K_a ) para varios ácidos comunes se dan en la Tabla ( PageIndex {1} ).
| Ácido | (HA ) | (K_a ) | (pK_a ) | (A ^ – ) | (K_b ) | (pK_b ) |
|---|---|---|---|---|---|---|
| * El número entre paréntesis indica el paso de ionización al que se hace referencia para un ácido poliprótico. | ||||||
| ácido hidroyódico | (HI ) | (2 por 10 ^ {9} ) | −9,3 | (I ^ – ) | (5,5 por 10 ^ {- 24} ) | 23,26 |
| ácido sulfúrico (1) * | (H_2SO_4 ) | (1 por 10 ^ {2} ) | −2,0 | (HSO_4 ^ – ) | (1 por 10 ^ {- 16} ) | 16,0 |
| ácido nítrico | (HNO_3 ) | (2,3 veces 10 ^ {1} ) | −1,37 | (NO_3 ^ – ) | (4,3 por 10 ^ {- 16} ) | 15,37 |
| ion hidronio | (H_3O ^ + ) | (1.0 ) | 0,00 | (H_2O ) | (1,0 veces 10 ^ {- 14} ) | 14,00 |
| ácido sulfúrico (2) * | (HSO_4 ^ – ) | (1.0 veces 10 ^ {- 2} ) | 1,99 | (SO_4 ^ {2 -} ) | (9.8 veces 10 ^ {- 13} ) | 12.01 |
| ácido fluorhídrico | (HF ) | (6,3 por 10 ^ {- 4} ) | 3,20 | (F ^ – ) | (1,6 veces 10 ^ {- 11} ) | 10,80 |
| ácido nitroso | (HNO_2 ) | (5,6 por 10 ^ {- 4} ) | 3,25 | (NO2 ^ – ) | (1,8 veces 10 ^ {- 11} ) | 10,75 |
| ácido fórmico | (HCO_2H ) | (1.78 veces 10 ^ {- 4} ) | 3.750 | (HCO_2− ) | (5,6 por 10 ^ {- 11} ) | 10.25 |
| ácido benzoico | (C_6H_5CO_2H ) | (6,3 por 10 ^ {- 5} ) | 4,20 | (C_6H_5CO_2 ^ – ) | (1,6 veces 10 ^ {- 10} ) | 9.80 |
| ácido acético | (CH_3CO_2H ) | (1,7 veces 10 ^ {- 5} ) | 4,76 | (CH_3CO_2 ^ – ) | (5,8 veces 10 ^ {- 10} ) | 9,24 |
| ion piridinio | (C_5H_5NH ^ + ) | (5,9 veces 10 ^ {- 6} ) | 5,23 | (C_5H_5N ) | (1,7 veces 10 ^ {- 9} ) | 8,77 |
| ácido hipocloroso | (HOCl ) | (4.0 veces 10 ^ {- 8} ) | 7,40 | (OCl ^ – ) | (2.5 veces 10 ^ {- 7} ) | 6,60 |
| ácido hidrocianico | (HCN ) | (6.2 veces 10 ^ {- 10} ) | 9,21 | (CN ^ – ) | (1,6 veces 10 ^ {- 5} ) | 4,79 |
| ion amonio | (NH_4 ^ + ) | (5,6 por 10 ^ {- 10} ) | 9,25 | (NH_3 ) | (1,8 veces 10 ^ {- 5} ) | 4,75 |
| agua | (H_2O ) | (1.0 veces 10 ^ {- 14} ) | 14,00 | (OH ^ – ) | (1,00 ) | 0,00 |
| acetileno | (C_2H_2 ) | (1 por 10 ^ {- 26} ) | 26,0 | (HC_2 ^ – ) | (1 por 10 ^ {12} ) | −12,0 |
| amoníaco | (NH_3 ) | (1 por 10 ^ {- 35} ) | 35,0 | (NH_2 ^ – ) | (1 por 10 ^ {21} ) | −21,0 |
Las bases débiles reaccionan con agua para producir el ion hidróxido, como se muestra en la siguiente ecuación general, donde B es la base original y BH + es su ácido conjugado:
[B _ {(aq)} + H_2O _ {(l)} rightleftharpoons BH ^ + _ {(aq)} + OH ^ −_ {(aq)} label {16.5.4} ] [19459010 ]
La constante de equilibrio para esta reacción es la constante de ionización de base (K b ), también llamada constante de disociación de base:
[K_b = K [H_2O] = frac {[BH ^ +] [OH ^ -]} {[B]} label {16.5.5} ]
Una vez más, la concentración de agua es constante, por lo que no aparece en la expresión de equilibrio constante; en su lugar, se incluye en (K_b ). Cuanto mayor sea (K_b ), más fuerte será la base y mayor será la concentración de (OH ^ – ) en el equilibrio. Los valores de (K_b ) para varias bases débiles comunes se dan en la Tabla ( PageIndex {2} ).
| Base | (B ) | (K_b ) | (pK_b ) | (BH ^ + ) | (K_a ) | (pK_a ) |
|---|---|---|---|---|---|---|
| * Como en la Tabla ( PageIndex {1} ). | ||||||
| ion hidróxido | (OH ^ – ) | (1.0 ) | 0,00 * | (H_2O ) | (1.0 veces 10 ^ {- 14} ) | 14,00 |
| ion fosfato | (PO_4 ^ {3 -} ) | (2.1 veces 10 ^ {- 2} ) | 1,68 | (HPO_4 ^ {2 -} ) | (4.8 veces 10 ^ {- 13} ) | 12.32 |
| dimetilamina | ((CH_3) _2NH ) | (5.4 veces 10 ^ {- 4} ) | 3.27 | ((CH_3) _2NH_2 ^ + ) | (1.9 veces 10 ^ {- 11} ) | 10,73 |
| metilamina | (CH_3NH_2 ) | (4,6 por 10 ^ {- 4} ) | 3,34 | (CH_3NH_3 ^ + ) | (2.2 veces 10 ^ {- 11} ) | 10,66 |
| trimetilamina | ((CH_3) _3N ) | (6,3 por 10 ^ {- 5} ) | 4,20 | ((CH_3) _3NH ^ + ) | (1,6 veces 10 ^ {- 10} ) | 9,80 |
| amoníaco | (NH_3 ) | (1,8 veces 10 ^ {- 5} ) | 4,75 | (NH_4 ^ + ) | (5,6 por 10 ^ {- 10} ) | 9,25 |
| piridina | (C_5H_5N ) | (1,7 veces 10 ^ {- 9} ) | 8,77 | (C_5H_5NH ^ + ) | (5.9 veces 10 ^ {- 6} ) | 5,23 |
| anilina | (C_6H_5NH_2 ) | (7,4 por 10 ^ {- 10} ) | 9,13 | (C_6H_5NH_3 ^ + ) | (1.3 veces 10 ^ {- 5} ) | 4,87 |
| agua | (H_2O ) | (1.0 veces 10 ^ {- 14} ) | 14,00 | (H_3O ^ + ) | (1.0 ^ * ) | 0,00 |
Hay una relación simple entre la magnitud de (K_a ) para un ácido y (K_b ) para su base conjugada. Considere, por ejemplo, la ionización del ácido hidrocianico ( (HCN )) en agua para producir una solución ácida, y la reacción de (CN ^ – ) con agua para producir una solución básica:
[HCN _ {(aq)} rightleftharpoons H ^ + _ {(aq)} + CN ^ −_ {(aq)} label {16.5.6} ]
[CN ^ −_ {(aq)} + H_2O _ {(l)} rightleftharpoons OH ^ −_ {(aq)} + HCN _ {(aq)} label {16.5.7} ] [19459010 ]
La expresión constante de equilibrio para la ionización de HCN es la siguiente:
[K_a = dfrac {[H ^ +] [CN ^ -]} {[HCN]} label {16.5.8} ]
La expresión correspondiente para la reacción de cianuro con agua es la siguiente:
[K_b = dfrac {[OH ^ -] [HCN]} {[CN ^ -]} label {16.5.9} ]
Si agregamos las ecuaciones ( ref {16.5.6} ) y ( ref {16.5.7} ), obtenemos lo siguiente:
| Reacción | Constantes de equilibrio |
|---|---|
| ( cancel {HCN _ {(aq)}} rightleftharpoons H ^ + _ {(aq)} + cancel {CN ^ −_ {(aq)}} ) | (K_a = [H ^ +] cancel {[CN ^ -]} / cancel {[HCN]} ) |
| ( cancel {CN ^ −_ {(aq)}} + H_2O _ {(l)} rightleftharpoons OH ^ −_ {(aq)} + cancel {HCN _ {(aq)}} ) [ 19459030] |
(K_b = [OH ^ -] cancel {[HCN]} / cancel {[CN ^ -]} ) |
| (H_2O _ {(l)} rightleftharpoons H ^ + _ {(aq)} + OH ^ −_ {(aq)} ) | (K = K_a veces K_b = [H ^ +] [OH ^ -] ) |
En este caso, la suma de las reacciones descritas por (K_a ) y (K_b ) es la ecuación para la autoionización del agua, y el producto de las dos constantes de equilibrio es (K_w ): [ 19459010]
[K_aK_b = K_w label {16.5.10} ]
Por lo tanto, si conocemos (K_a ) para un ácido o (K_b ) para su base conjugada, podemos calcular la otra constante de equilibrio para cualquier par ácido-base conjugado.
Al igual que con (pH ), (pOH ) y pKw, podemos usar logaritmos negativos para evitar la notación exponencial al escribir constantes de ionización de ácido y base, definiendo (pK_a ) de la siguiente manera: [19459010 ]
[pKa = – log_ {10} K_a label {16.5.11} ]
[K_a = 10 ^ {- pK_a} label {16.5.12} ]
y (pK_b ) como
[pK_b = – log_ {10} K_b label {16.5.13} ]
[K_b = 10 ^ {- pK_b} label {16.5.14} ]
Del mismo modo, la ecuación ( ref {16.5.10} ), que expresa la relación entre (K_a ) y (K_b ), se puede escribir en forma logarítmica de la siguiente manera:
[pK_a + pK_b = pK_w label {16.5.15} ]
A 25 ° C, esto se convierte en
[pK_a + pK_b = 14.00 label {16.5.16} ]
Los valores de (pK_a ) y (pK_b ) se dan para varios ácidos y bases comunes en las Tablas ( PageIndex {1} ) y ( PageIndex {2} ), respectivamente, y Se proporciona un conjunto más extenso de datos en las Tablas E1 y E2. Debido al uso de logaritmos negativos, los valores más pequeños de (pK_a ) corresponden a constantes de ionización de ácido más grandes y, por lo tanto, ácidos más fuertes. Por ejemplo, el ácido nitroso ( (HNO_2 )), con un (pK_a ) de 3.25, es aproximadamente un millón de veces más ácido que el ácido hidrocianico (HCN), con un (pK_a ) de 9.21. Por el contrario, los valores más pequeños de (pK_b ) corresponden a constantes de ionización de bases más grandes y, por lo tanto, a bases más fuertes.
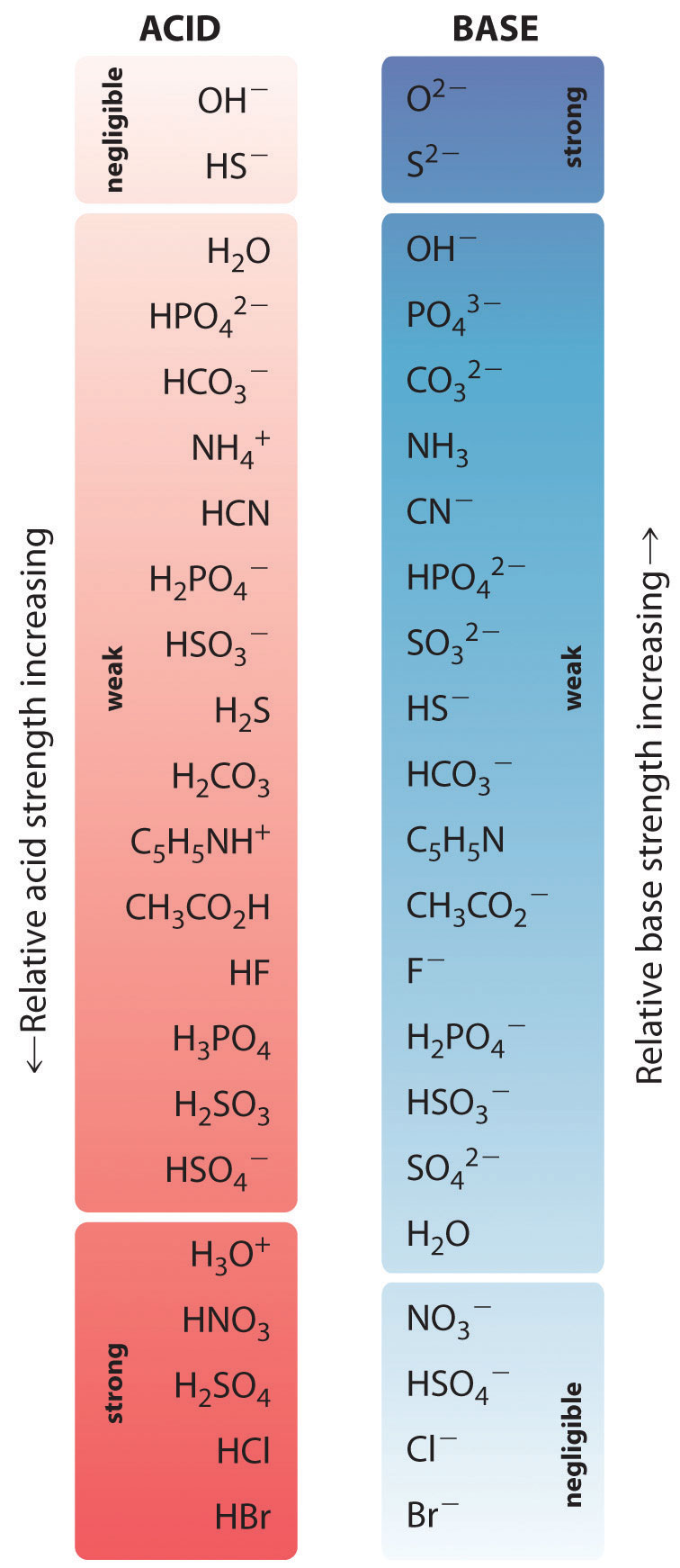
Las fuerzas relativas de algunos ácidos comunes y sus bases conjugadas se muestran gráficamente en la Figura ( PageIndex {1} ). Los pares conjugados ácido-base se enumeran en orden (de arriba a abajo) de mayor intensidad de ácido, que corresponde a valores decrecientes de (pK_a ). Este orden corresponde a la fuerza decreciente de la base conjugada o al aumento de los valores de (pK_b ). En la parte inferior izquierda de la Figura ( PageIndex {2} ) están los ácidos fuertes comunes; en la parte superior derecha están las bases fuertes más comunes. Observe la relación inversa entre la fuerza del ácido parental y la fuerza de la base conjugada. Así, la base conjugada de un ácido fuerte es una base muy débil, y la base conjugada de un ácido muy débil es una base fuerte.
La base conjugada de un ácido fuerte es una base débil y viceversa.
Podemos usar las fuerzas relativas de ácidos y bases para predecir la dirección de una reacción ácido-base siguiendo una sola regla: un equilibrio ácido-base siempre favorece el lado con el ácido y la base más débiles, como lo indican estas flechas :
[ text {ácido más fuerte + base más fuerte} ce {<= >>} text {ácido más débil + base más débil} ]
En una reacción ácido-base, el protón siempre reacciona con la base más fuerte.
Por ejemplo, el ácido clorhídrico es un ácido fuerte que se ioniza esencialmente por completo en solución acuosa diluida para producir (H_3O ^ + ) y (Cl ^ – ); solo cantidades insignificantes de moléculas de (HCl ) permanecen sin disociar. Por lo tanto, el equilibrio de ionización se encuentra prácticamente a la derecha, representado por una sola flecha:
[HCl _ {(aq)} + H_2O _ {(l)} rightarrow H_3O ^ + _ {(aq)} + Cl ^ −_ {(aq)} label {16.5.17} ] [19459010 ]
En contraste, el ácido acético es un ácido débil y el agua es una base débil. En consecuencia, las soluciones acuosas de ácido acético contienen principalmente moléculas de ácido acético en equilibrio con una pequeña concentración de (H_3O ^ + ) y iones acetato, y el equilibrio de ionización se encuentra muy a la izquierda, como se representa por estas flechas:
[ ce {CH_3CO_2H _ {(aq)} + H_2O _ {(l)} << => H_3O ^ + _ {(aq)} + CH_3CO_ {2 (aq)} ^ -} ]
De manera similar, en la reacción de amoníaco con agua, el ion hidróxido es una base fuerte, y el amoníaco es una base débil, mientras que el ion amonio es un ácido más fuerte que el agua. Por lo tanto, este equilibrio también se encuentra a la izquierda:
[H_2O _ {(l)} + NH_ {3 (aq)} ce {<< =>} NH ^ + _ {4 (aq)} + OH ^ -_ {(aq)} ] [ 19459010]
Todos los equilibrios ácido-base favorecen el lado con el ácido y la base más débiles. Por lo tanto, el protón está unido a la base más fuerte.
Soluciones de ácidos y bases fuertes: el efecto nivelador
Notará en la Tabla ( PageIndex {1} ) que los ácidos como (H_2SO_4 ) y (HNO_3 ) se encuentran por encima del ion hidronio, lo que significa que tienen valores de (pK_a ) menores que cero y son ácidos más fuertes que el ion (H_3O ^ + ). Recuerde del Capítulo 4 que el protón ácido en prácticamente todos los oxoácidos está unido a uno de los átomos de oxígeno del oxoanión. Por lo tanto, el ácido nítrico debe escribirse correctamente como (HONO_2 ). Desafortunadamente, sin embargo, las fórmulas de los oxoácidos casi siempre se escriben con hidrógeno a la izquierda y oxígeno a la derecha, dando (HNO_3 ) en su lugar. De hecho, los seis ácidos fuertes comunes que encontramos por primera vez en el Capítulo 4 tienen valores de (pK_a ) menores que cero, lo que significa que tienen una mayor tendencia a perder un protón que el (H_3O ^ + ) ion. Por el contrario, las bases conjugadas de estos ácidos fuertes son bases más débiles que el agua. En consecuencia, los equilibrios de transferencia de protones para estos ácidos fuertes se encuentran muy a la derecha, y la adición de cualquiera de los ácidos fuertes comunes al agua da como resultado una reacción esencialmente estequiométrica del ácido con agua para formar una solución de (H_3O ^ + ) ion y la base conjugada del ácido.
Aunque (K_a ) para (HI ) es aproximadamente 108 mayor que (K_a ) para (HNO_3 ), la reacción de (HI ) o (HNO_3 ) con agua da una solución esencialmente estequiométrica de (H_3O ^ + ) e I− o (NO_3 ^ – ). De hecho, una solución acuosa 0.1 M de cualquier ácido fuerte en realidad contiene 0.1 M (H_3O ^ + ), independientemente de la identidad del ácido fuerte. Este fenómeno se denomina efecto nivelador: cualquier especie que sea un ácido más fuerte que el ácido conjugado del agua ( (H_3O ^ + )) se nivela a la fuerza de (H_3O ^ + ) en solución acuosa porque (H_3O ^ + ) es el ácido más fuerte que puede existir en equilibrio con el agua. En consecuencia, es imposible distinguir entre las concentraciones de ácidos tales como HI y HNO3 en solución acuosa, y se debe utilizar un enfoque alternativo para determinar sus concentraciones de ácido relativas.
Un método es usar un solvente tal como ácido acético anhidro. Debido a que el ácido acético es un ácido más fuerte que el agua, también debe ser una base más débil, con una menor tendencia a aceptar un protón que (H_2O ). Las mediciones de la conductividad de soluciones 0.1 M de HI y (HNO_3 ) en ácido acético muestran que HI está completamente disociado, pero (HNO_3 ) está solo parcialmente disociado y se comporta como un ácido débil en este solvente. Este resultado nos dice claramente que HI es un ácido más fuerte que (HNO_3 ). El orden relativo de las concentraciones de ácido y los valores aproximados de (K_a ) y (pK_a ) para los ácidos fuertes en la parte superior de la Tabla ( PageIndex {1} ) se determinaron utilizando medidas como esta y diferentes solventes no acuosos.
En soluciones acuosas , (H_3O ^ + ) es el ácido más fuerte y (OH ^ – ) es la base más fuerte que puede existir en equilibrio con (H_2O ).
El efecto de nivelación se aplica también a soluciones de bases fuertes: en una solución acuosa, cualquier base más fuerte que OH− se nivela a la fuerza de OH− porque OH− es la base más fuerte que puede existir en equilibrio con agua. Sales como (K_2O ), (NaOCH_3 ) (metóxido de sodio) y (NaNH_2 ) (sodamida o amida de sodio), cuyos aniones son las bases conjugadas de especies que se encuentran debajo del agua en la Tabla ( PageIndex {2} ), son todas bases fuertes que reaccionan esencialmente completamente (y a menudo violentamente) con agua, aceptando un protón para dar una solución de (OH ^ – ) y el catión correspondiente:
[K_2O _ {(s)} + H_2O _ {(l)} rightarrow 2OH ^ −_ {(aq)} + 2K ^ + _ {(aq)} label {16.5.18} ] [19459010 ]
[NaOCH_ {3 (s)} + H_2O _ {(l)} rightarrow OH ^ −_ {(aq)} + Na ^ + _ {(aq)} + CH_3OH _ {(aq)} label { 16.5.19} ]
[NaNH_ {2 (s)} + H_2O _ {(l)} rightarrow OH ^ −_ {(aq)} + Na ^ + _ {(aq)} + NH_ {3 (aq)} label {16.5.20} ]
Otros ejemplos que puede encontrar son hidruro de potasio ( (KH )) y compuestos organometálicos como el metil litio ( (CH_3Li )).
Ácidos y bases polipróticos
Como aprendiste, los ácidos polipróticos como (H_2SO_4 ), (H_3PO_4 ) y (H_2CO_3 ) contienen más de un protón ionizable, y los protones se pierden de forma gradual. La especie totalmente protonada es siempre el ácido más fuerte porque es más fácil eliminar un protón de una molécula neutra que de un ion cargado negativamente. Por lo tanto, la fuerza del ácido disminuye con la pérdida de protones posteriores y, en consecuencia, aumenta (pK_a ). Considere (H_2SO_4 ), por ejemplo:
[HSO ^ −_ {4 (aq)} ce {<= >>} SO ^ {2 -} _ {4 (aq)} + H ^ + _ {(aq)} ; ; ; pK_a = -2 ]
El equilibrio en la primera reacción se encuentra muy a la derecha, consistente con (H_2SO_4 ) siendo un ácido fuerte. En contraste, en la segunda reacción, cantidades apreciables de (HSO_4 ^ – ) y (SO_4 ^ {2 -} ) están presentes en el equilibrio.
Para un ácido poliprótico, la fuerza del ácido disminuye y el (pK_a ) aumenta con la pérdida secuencial de cada protón.
El ion sulfato de hidrógeno ( (HSO_4 ^ – )) es tanto la base conjugada de (H_2SO_4 ) como el ácido conjugado de (SO_4 ^ {2 -} ). Al igual que el agua, el HSO4− puede actuar como un ácido o una base, dependiendo de si el otro reactivo es un ácido más fuerte o una base más fuerte. Por el contrario, el ion sulfato ( (SO_4 ^ {2 -} )) es una base poliprótica que es capaz de aceptar dos protones de manera gradual:
[SO ^ {2 -} _ {4 (aq)} + H_2O _ {(aq)} ce {<= >>} HSO ^ {-} _ {4 (aq)} + OH _ {(aq )} ^ – ]
[HSO ^ {-} _ {4 (aq)} + H_2O _ {(aq)} ce {<= >>} H_2SO_ {4 (aq)} + OH _ {(aq)} ^ – label {16.6} ]
Al igual que cualquier otro par conjugado ácido-base, las fuerzas de los ácidos y bases conjugados están relacionadas por (pK_a ) + (pK_b ) = pKw. Considere, por ejemplo, el par conjugado ácido (HSO_4 ^ – / SO_4 ^ {2 -} ) conjugado. En la Tabla ( PageIndex {1} ), vemos que el (pK_a ) de (HSO_4 ^ – ) es 1.99. Por lo tanto, el (pK_b ) de (SO_4 ^ {2 -} ) es 14.00 – 1.99 = 12.01. Por lo tanto, el sulfato es una base bastante débil, mientras que (OH ^ – ) es una base fuerte, por lo que el equilibrio que se muestra en la ecuación ( ref {16.6} ) se encuentra a la izquierda. El ion (HSO_4 ^ – ) también es una base muy débil ( (pK_a ) de (H_2SO_4 ) = 2.0, (pK_b ) de (HSO_4 ^ – = 14 – (−2.0) = 16 )), que es consistente con lo que esperamos para la base conjugada de un ácido fuerte.
Resumen
Las reacciones ácido-base siempre contienen dos pares conjugados de ácido-base. Cada ácido y cada base tiene una constante de ionización asociada que corresponde a su fuerza de ácido o base. Dos especies que se diferencian solo por un protón constituyen un par conjugado ácido-base. La magnitud de la constante de equilibrio para una reacción de ionización se puede usar para determinar las fuerzas relativas de ácidos y bases. Para una solución acuosa de un ácido débil, la constante de disociación se llama constante de ionización ácida ( (K_a )). De manera similar, la constante de equilibrio para la reacción de una base débil con agua es la constante de ionización de base ( (K_b )). Para cualquier par conjugado ácido-base, (K_aK_b = K_w ). Smaller values of (pK_a) correspond to larger acid ionization constants and hence stronger acids. Conversely, smaller values of (pK_b) correspond to larger base ionization constants and hence stronger bases. At 25°C, (pK_a + pK_b = 14.00). Acid–base reactions always proceed in the direction that produces the weaker acid–base pair. No acid stronger than (H_3O^+) and no base stronger than (OH^−) can exist in aqueous solution, leading to the phenomenon known as the leveling effect. Polyprotic acids (and bases) lose (and gain) protons in a stepwise manner, with the fully protonated species being the strongest acid and the fully deprotonated species the strongest base.
Key Equations
- Acid ionization constant: [K_a=K[H_2O]=dfrac{[H_3O^+][A^−]}{[HA]} ]
- Base ionization constant: [K_b=K[H_2O]= dfrac{[BH^+][OH^−]}{[B]} ]
- Relationship between (K_a) and (K_b) of a conjugate acid–base pair: [K_aK_b = K_w ]
- Definition of (pK_a): [pKa = −log_{10}K_a ] [K_a=10^{−pK_a} ]
- Definition of (pK_b): [pK_b = −log_{10}K_b ] [K_b=10^{−pK_b} ]
- Relationship between (pK_a) and (pK_b) of a conjugate acid–base pair: [pK_a + pK_b = pK_w ] [pK_a + pK_b = 14.00 ; text{at 25°C} ]