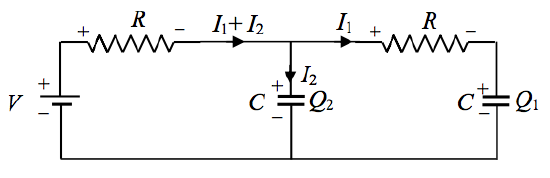
( text {FIGURE XIV.1} )
El circuito de la figura ( text {XIV.1} ) contiene dos resistencias iguales, dos capacitancias iguales y una batería. La batería está conectada en el momento (t = 0 ). Encuentre las cargas retenidas por los condensadores después del tiempo (t ).
Aplica la segunda regla de Kirchhoff a cada mitad:
[( dot Q_1 + dot Q_2) RC + Q_2 = CV, tag {14.12.1} ]
y [ dot Q_1 RC + Q_1 – Q_2 = 0. tag {14.12.2} ] [ 19459035]
Eliminar (Q_2 ):
[R ^ 2C ^ 2 ddot Q_1 + 3 RC Q_1 + Q_1 = CV. tag {14.12.3} ]
Transformar, con (Q_1 ) y ( dot Q_1 ) inicialmente cero:
[ 19459036] [(R ^ 2C ^ 2s ^ 2 + 3RCs + 1) bar {Q_1} = frac {CV} {s}. Tag {14.12.4} ]
Es decir [R ^ 2C bar {Q_1} = frac {1} {s (s ^ 2 + 3as + a ^ 2)} cdot V, tag {14.12.5} ] [ 19459031]
donde [a = 1 / (RC). tag {14.12.6} ]
Eso es [R ^ 2C bar {Q_1} = frac {1} {s (s + 2.618a) (s + 0.382a)} V. tag {14.12.7} ]
Fracciones parciales: [R ^ 2C bar {Q_1} = left [ frac {1} { s} + frac {0.1708} {s + 2.618a} – frac {1.1708} {s + 0.382a} right] frac {V} {a ^ 2}. tag {14.12.8} ]
Es decir, [ bar {Q_1} = left [ frac {1} {s} + frac {0.1708} {s + 2.618a} – frac {1.1708} {s + 0.382a} right] CV. tag {14.12.9} ]
Transformación inversa: [Q_1 = left [1 + 0.1708e ^ {- 2.618t / (RC) } – 1.1708e ^ {- 0.382t / (RC)} right]. tag {14.12.10} ]
La corriente se puede encontrar por diferenciación.
Le dejo al lector eliminar (Q_1 ) de las ecuaciones 14.12.1 y 2 y, por lo tanto, mostrar que [ 19459031]
[Q_2 = left [1 – 0.2764 e ^ {- 2.618 t / (RC)} – 0.7236 e ^ {- 0.382 t / (RC)} right]. tag {14.12.11} ]