En Sección 5.19 conectamos una batería a una capacitancia y una resistencia en serie para ver cómo la corriente en el circuito y la carga en el capacitor variaban con el tiempo; En este capítulo, Sección 10.12 , conectamos una batería a una inductancia y una resistencia en serie para ver cómo la corriente aumentaba con el tiempo. Todavía no hemos conectado una batería a (R ), (C ), (L ) en serie. Estamos a punto de hacer esto. También recordamos, de Sección 5.19 , cuando conectamos una batería a (C ) y (R ) en serie, la corriente aparentemente aumenta instantáneamente de cero a (E / R ) como Tan pronto como cerramos el interruptor. Señalamos que cualquier circuito real (que es necesariamente un bucle) debe tener cierta inductancia, por pequeña que sea, y en consecuencia la corriente tarda un tiempo finito, por pequeño que sea, en alcanzar su valor máximo después de cerrar el interruptor.
La ecuación diferencial que muestra cómo el EMF de la batería es igual a la suma de las diferencias potenciales entre los tres elementos es
[ label {10.15.1} E = IR + Q / C + L dot I ]
Si escribimos (L = dot Q text {y} dot I = ddot Q ) llegamos a la ecuación diferencial para la carga en el condensador:
[ label {10.15.2} LC ddot Q + RC dot Q + Q = EC ]
Las soluciones generales para esto son las mismas que para la ecuación 10.14.2, excepto por la suma de la integral particular, que los devotos de ecuaciones diferenciales reconocerán simplemente (EC ). Las soluciones generales para el actual I se pueden encontrar diferenciando las soluciones para (Q ) con respecto al tiempo.
Así, las soluciones generales son
Si la resistencia es menor que (2 sqrt { frac {L} {C}} ) la carga en el condensador y la corriente en el circuito serán variar con el tiempo como
[ label {10.15.3} Q = Le ^ {- gamma T} sin ( omega ^ prime t + alpha) + EC. ]
[ label {10.15.4} I = Ke ^ {- gamma t} [ omega ^ prime + alpha) – gamma sin ( omega ^ prime t + alpha)]. ]
Las definiciones de las constantes ( gamma text {y} omega ^ prime ) fueron dadas por las ecuaciones 10.14.4.
Si la resistencia es mayor que (2 sqrt { frac {L} {C}} ) la carga en el condensador y la corriente en el circuito variar con el tiempo como
[ label {10.15.5} Q = Ae ^ {- lambda_1t} + Be ^ {- lambda_2t} + EC. ]
[ label {10.15.6} I = – ( lambda_1Ae ^ {- lambda_1t} + lambda_2Be ^ {- lambda_2t}). ]
Las definiciones de las constantes ( lambda_1 text {y} lambda_2 ) fueron dadas por las ecuaciones 10.14.7.
Si la resistencia es igual a (2 sqrt { frac {L} {C}} ) la carga en el condensador y la corriente en el circuito variará con el tiempo como
[ label {10.15.7} Q = Ke ^ {- frac {Rt} {2L}} (1 + at) + EC. ]
[ label {10.15.8} I = Ke ^ {- frac {Rt} {2L}} left [a- frac {R} {2L} (1-at) right]. ]
Las constantes de integración se pueden encontrar a partir de las condiciones iniciales. En (t = 0, , Q ), la carga en el condensador es cero. (Esto es diferente del ejemplo en Sección 10.14 , donde la carga inicial era (Q_0 ). También en (t = 0 ), la corriente (I = 0 ). De hecho esto es una de las motivaciones para hacer esta investigación: recuerde nuestra dificultad en la Sección 5.19. Los resultados de aplicar las condiciones iniciales son:
Si la resistencia es mayor que (2 sqrt { frac {L} {C}} ) las constantes de integración están dadas por
[ label {10.15.10} tan alpha = frac { omega ^ prime} { gamma} ]
y
[ label {10.15.11} K = – frac {EC} { sin alpha} ]
En principio, estos podrían insertarse en las ecuaciones ref {10.15.3} y ref {10.15.4}. Para fines computacionales, es más fácil dejar las ecuaciones como están.
Si la resistencia es mayor que (2 sqrt { frac {L} {C}} ) la carga en el condensador y la corriente en el circuito variar con el tiempo como
[ label {10.15.12} Q = EC left [1- left ( frac { lambda_2 e ^ {- lambda_1 t} – lambda_1e ^ {- lambda_2t}} { lambda_2 – lambda_1} right) right] ]
[ label {10.15.13} I = EC left ( frac { lambda_1 lambda_2} { lambda_2 – lambda_1} right) left (e ^ {- lambda_1t} -e ^ { – lambda_2t} right). ]
Si la resistencia es igual a (2 sqrt { frac {L} {C}} ) la carga en el condensador y la corriente en el circuito variar con el tiempo como
[ label {10.15.14} Q = EC left [1-e ^ {- Rt / (2L)} left (1+ frac {Rt} {2L} right) right] ]
[ label {10.15.15} I = frac {ECR ^ 2} {4L ^ 2} te ^ {- Rt / (2L)}. ]
Se notará, en los tres casos, que la función complementaria de la solución a la ecuación diferencial es un transitorio que eventualmente desaparece, mientras que la integral particular representa la solución final de estado estable . Los lectores pueden haber notado que, cuando se funde un fusible, a menudo se funde justo cuando se enciende; Es la oleada transitoria la que da el golpe fatal.
La situación que inicialmente nos interesó en este problema fue cuando la inductancia en el circuito era muy pequeña, es decir, cuando la resistencia es mayor que (2 sqrt { frac {L} {C}} ) Nos preocupaba que, cuando la inductancia fuera realmente cero, la corriente aparentemente aumentó inmediatamente a (EC ) tan pronto como se cerró el interruptor. Así que veamos la ecuación ref {10.15.13}. Si multiplicamos ambos lados por (CR ), se puede escribir en forma adimensional como
[ label {10.15.16} frac {I} {E / R} = left ( frac {l_1 l_2} {l_2-l_1} right) left (e ^ {- l_1 tau } -e ^ {- l_2 tau} right), ]
donde
[ label {10.15.17} tau = t / (CR) quad text {y} quad l_i = CR lambda_i. ]
En otras palabras, estamos expresando el tiempo en unidades de (CR ).
Se puede observar, mediante la diferenciación de la ecuación ref {10.15.16}, que la corriente alcanzará un valor máximo (que es menor que (E / R )) en el tiempo dado por
[ label {10.15.18} tau = frac { ln (l_2 / l_1)} {l_2-l_1} = frac { ln ( lambda_2 / lambda_1)} { lambda_2- lambda_1}. ]
Las dos constantes ( lambda ), definidas por primera vez en las ecuaciones 10.14.7, se pueden escribir en la forma
[ label {10.15.19} lambda_1 = frac {R} {2L} left [1- sqrt {1- frac {4 (L / R)} {RC}} right] , , lambda_2 = frac {R} {2L} left [1+ sqrt {1- frac {4 (L / R)} {RC}} right] ]
Presento la relación adimensional
[ label {10.15.20} x = frac {L / R} {CR}, ]
para que
[ label {10.15.21} l_1 = frac {1- sqrt {1-4x}} {2x}, quad l_2 = frac {1+ sqrt {1-4x}} {2x } ]
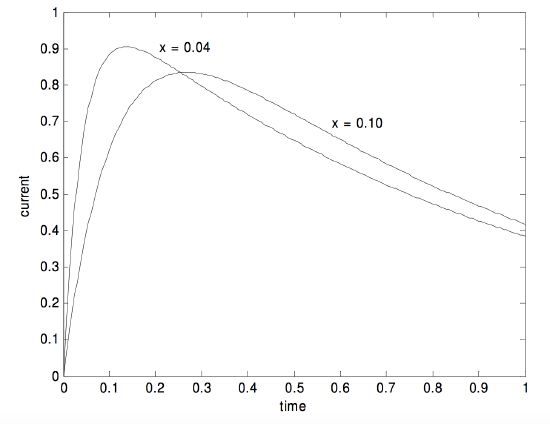
En la tabla y el gráfico a continuación, muestro cómo cambia la (I ) actual con el tiempo (ecuación ref {10.15.13} o, en forma adimensional, ref {10.15.16}) para (x = frac {1} {10} ) y para (x = frac {1} {25} ). La corriente se da en unidades de (E / R ), y el tiempo está en unidades de (RC ). Solo si la inductancia del circuito es exactamente cero (que no puede obtenerse en ningún circuito cerrado real) la corriente saltará inmediatamente de 0 a (E / R ) en el instante en que el interruptor esté cerrado.
[ nonumber begin {matrix} x & l_1 & l_2 & frac {l_1l_2} {l_2-l_1} & tau_ {max} & frac {I_ {max}} {E / R} \ nonumber \ nonumber 0.10 y 1.12702 y 8.87298 y 1.29099 y 0.26639 y 0.83473 \ nonumber 0.04 y 1.04356 y 23.95644 y 1.09109 y 0.13676 y 0.90476 \ end {matrix} ]