Si sueltas tu zapato y una moneda uno al lado del otro, caen al suelo al mismo tiempo. ¿Por qué el zapato no llega allí primero, ya que la gravedad está presionando más? ¿Cómo funciona la lente de su ojo y por qué los músculos de su ojo necesitan aplastar su lente en diferentes formas para enfocar objetos cercanos o lejanos? Este es el tipo de preguntas que la física intenta responder sobre el comportamiento de la luz y la materia, las dos cosas de las que está hecho el universo.
Hasta hace muy poco en la historia, no se avanzó en responder preguntas como estas. Peor que eso, las respuestas incorrectas escritas por pensadores como el físico griego antiguo Aristóteles fueron aceptadas sin cuestionamientos durante miles de años. ¿Por qué el conocimiento científico ha progresado más desde el Renacimiento que en todos los milenios anteriores desde el comienzo de la historia registrada? Sin duda, la revolución industrial es parte de la respuesta. La construcción de su pieza central, la máquina de vapor, requería técnicas mejoradas para una construcción y medición precisas. (Al principio, se consideraba un avance importante cuando los talleres de maquinaria ingleses aprendieron a construir pistones y cilindros que encajaban con un espacio más estrecho que el grosor de un centavo). Pero incluso antes de la revolución industrial, el ritmo del descubrimiento había aumentado, principalmente debido a la introducción del método científico moderno. Aunque evolucionó con el tiempo, la mayoría de los científicos de hoy estarían de acuerdo en algo como la siguiente lista de los principios básicos del método científico:
(1) La ciencia es un ciclo de teoría y experimento. Las teorías científicas se crean para explicar los resultados de los experimentos que se crearon bajo ciertas condiciones. Una teoría exitosa también hará nuevas predicciones sobre nuevos experimentos bajo nuevas condiciones. Eventualmente, sin embargo, siempre parece suceder que surge un nuevo experimento, que muestra que bajo ciertas condiciones la teoría no es una buena aproximación o no es válida en absoluto. La pelota vuelve a la cancha de teóricos. Si un experimento no está de acuerdo con la teoría actual, la teoría debe cambiarse, no el experimento.

a / La ciencia es un ciclo de teoría y experimento.

b / Un dibujo satírico del laboratorio de un alquimista. H. Cock, según un dibujo de Peter Brueghel el Viejo (siglo XVI).
(2) Las teorías deben predecir y explicar. El requisito de poder predictivo significa que una teoría solo es significativa si predice algo que puede verificarse contra mediciones experimentales que el teórico aún no tenía a la mano. Es decir, una teoría debería ser comprobable. El valor explicativo significa que muchos fenómenos deben explicarse con pocos principios básicos. Si responde a todas las preguntas de “por qué” con “porque así son las cosas”, entonces su teoría no tiene valor explicativo. Recopilar muchos datos sin poder encontrar ningún principio básico subyacente no es ciencia.
(3) Los experimentos deben ser reproducibles. Un experimento debe tratarse con sospecha si solo funciona para una persona, o solo en una parte del mundo. Cualquier persona con las habilidades y el equipo necesarios debería poder obtener los mismos resultados del mismo experimento. Esto implica que la ciencia trasciende las fronteras nacionales y étnicas; puede estar seguro de que nadie está haciendo ciencia real que afirme que su trabajo es “ario, no judío”, “marxista, no burgués” o “cristiano, no ateo”. Un experimento no puede reproducirse si es secreto, por lo que la ciencia es necesariamente una empresa pública.
Como ejemplo del ciclo de teoría y experimento, un paso vital hacia la química moderna fue la observación experimental de que los elementos químicos no podían transformarse entre sí, por ejemplo, el plomo no podía convertirse en oro. Esto condujo a la teoría de que las reacciones químicas consistían en reordenamientos de los elementos en diferentes combinaciones, sin ningún cambio en las identidades de los elementos mismos. La teoría funcionó durante cientos de años y se confirmó experimentalmente en un amplio rango de presiones y temperaturas y con muchas combinaciones de elementos. Solo en el siglo XX supimos que un elemento podía transformarse en otro bajo las condiciones de presión y temperatura extremadamente altas que existen en una bomba nuclear o dentro de una estrella. Esa observación no invalidó por completo la teoría original de la inmutabilidad de los elementos, pero demostró que era solo una aproximación, válida a temperaturas y presiones normales.
autocomprobación:
Un psíquico conduce sesiones en las que los espíritus de los muertos hablan con los participantes. Él dice que tiene poderes psíquicos especiales que no poseen otras personas, lo que le permite “canalizar” las comunicaciones con los espíritus. ¿Qué parte del método científico se está violando aquí?
(respuesta en la parte posterior de la versión PDF del libro)
El método científico como se describe aquí es una idealización, y no debe entenderse como un procedimiento establecido para hacer ciencia . Los científicos tienen tantas debilidades y defectos de carácter como cualquier otro grupo, y es muy común que los científicos traten de desacreditar los experimentos de otras personas cuando los resultados son contrarios a su propio punto de vista favorito. La ciencia exitosa también tiene más que ver con la suerte, la intuición y la creatividad de lo que la mayoría de las personas se dan cuenta, y las restricciones del método científico no sofocan la individualidad y la autoexpresión más de lo que las formas de fuga y sonata sofocaron a Bach y Haydn. Existe una tendencia reciente entre los científicos sociales de ir aún más lejos y negar que el método científico exista, alegando que la ciencia no es más que un sistema social arbitrario que determina qué ideas aceptar según los criterios de un grupo. Creo que eso va demasiado lejos. Si la ciencia es un ritual social arbitrario, parecería difícil explicar su efectividad en la construcción de elementos útiles como aviones, reproductores de CD y alcantarillas. Si la alquimia y la astrología no fueran menos científicas en sus métodos que la química y la astronomía, ¿qué fue lo que les impidió producir algo útil?
Preguntas de discusión
◊ Considere si el método científico se está aplicando o no en los siguientes ejemplos. Si el método científico no se aplica, ¿las personas cuyas acciones se describen realizan una actividad humana útil, aunque no científica?
◊ La acupuntura es una técnica médica tradicional de origen asiático en la que se insertan pequeñas agujas en el cuerpo del paciente para aliviar el dolor. Muchos médicos capacitados en el oeste consideran que la acupuntura no es digna de estudio experimental porque si tuviera efectos terapéuticos, tales efectos no podrían explicarse por sus teorías del sistema nervioso. ¿Quién está siendo más científico, los practicantes occidentales u orientales?
◊ Goethe, un poeta alemán, es menos conocido por su teoría del color. Publicó un libro sobre el tema, en el que argumentó que el aparato científico para medir y cuantificar el color, como prismas, lentes y filtros de colores, no podía darnos una idea completa del significado último del color, por ejemplo, la sensación de frío provocada por azul y verde o los sentimientos heroicos inspirados en el rojo. ¿Fue su trabajo científico?
◊ Un niño pregunta por qué las cosas se caen, y un adulto responde “debido a la gravedad”. El antiguo filósofo griego Aristóteles explicó que las rocas cayeron porque era su naturaleza buscar su lugar natural, en contacto con la tierra. ¿Son científicas estas explicaciones?
◊ El budismo es en parte una explicación psicológica del sufrimiento humano, y la psicología es, por supuesto, una ciencia. Se podría decir que el Buda se involucró en un ciclo de teoría y experimento, ya que trabajó por ensayo y error, e incluso al final de su vida, pidió a sus seguidores que desafiaran sus ideas. El budismo también podría considerarse reproducible, ya que el Buda les dijo a sus seguidores que podrían encontrar la iluminación por sí mismos si seguían un cierto curso de estudio y disciplina. ¿Es el budismo una búsqueda científica?
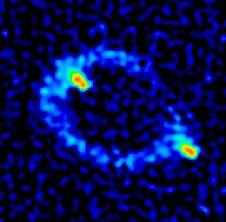
c / Esta imagen del telescopio muestra dos imágenes del mismo objeto distante, un objeto exótico y muy luminoso llamado cuásar. Esto se interpreta como evidencia de que un objeto masivo y oscuro, posiblemente un agujero negro, está entre nosotros y él. Los rayos de luz que de otro modo habrían perdido la tierra a ambos lados han sido doblados por la gravedad del objeto oscuro para que nos alcancen. La dirección real hacia el quásar es presumiblemente en el centro de la imagen, pero la luz a lo largo de esa línea central no nos llega porque es absorbida por el objeto oscuro. El quásar es conocido por su número de catálogo, MG1131 + 0456, o más informalmente como el Anillo de Einstein.
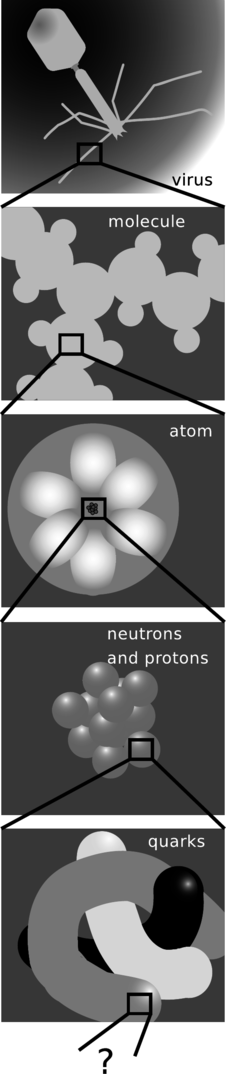
d / Reduccionismo.
0.1.2 ¿Qué es la física?
Dada por un instante una inteligencia que podría comprender todas las fuerzas por las cuales la naturaleza se anima y las posiciones respectivas de las cosas que la componen … nada sería incierto, y el futuro como el pasado estaría establecido fuera ante sus ojos. – Pierre Simon de Laplace
La física es el uso del método científico para descubrir los principios básicos que rigen la luz y la materia, y descubrir las implicaciones de esas leyes. Parte de lo que distingue la perspectiva moderna de la mentalidad antigua es la suposición de que existen reglas por las cuales funciona el universo, y que esas leyes pueden ser entendidas al menos parcialmente por los humanos. Desde la Era de la Razón hasta el siglo XIX, muchos científicos comenzaron a convencerse de que las leyes de la naturaleza no solo podían conocerse, sino que, como afirma Laplace, esas leyes podrían, en principio, usarse para predecir todo sobre el futuro del universo si la información completa estaba disponible sobre el estado actual de toda la luz y la materia. En las secciones siguientes, describiré dos tipos generales de limitaciones en la predicción utilizando las leyes de la física, que solo se reconocieron en el siglo XX.
La materia se puede definir como cualquier cosa que se vea afectada por la gravedad, es decir, que tenga peso o lo tendría si estuviera cerca de la Tierra u otra estrella o planeta lo suficientemente masivo como para producir una gravedad medible. La luz se puede definir como cualquier cosa que puede viajar de un lugar a otro a través del espacio vacío y puede influir en la materia, pero no tiene peso. Por ejemplo, la luz solar puede influir en su cuerpo al calentarlo o dañar su ADN y provocarle cáncer de piel. La definición física de la luz incluye una variedad de fenómenos que no son visibles para el ojo, incluidas ondas de radio, microondas, rayos X y rayos gamma. Estos son los “colores” de la luz que no se encuentran dentro del estrecho rango violeta a rojo del arco iris que podemos ver.
autocomprobación:
A principios del siglo XX, se descubrió un fenómeno nuevo y extraño en los tubos de vacío: misterioso rayos de origen y naturaleza desconocidos. Estos rayos son los mismos que se disparan desde la parte posterior del tubo de imagen de su televisor y golpean la parte delantera para hacer la imagen. Los físicos en 1895 no tenían la menor idea de qué eran los rayos, por lo que simplemente los llamaron “rayos catódicos”, por el nombre del contacto eléctrico del que surgieron. Se produjo un feroz debate, completo con connotaciones nacionalistas, sobre si los rayos eran una forma de luz o de materia. ¿Qué habrían tenido que hacer para resolver el problema?
(respuesta al final de la versión PDF del libro)
Muchos fenómenos físicos no son luz o materia, sino propiedades de la luz o la materia o interacciones entre la luz y importar. Por ejemplo, el movimiento es una propiedad de toda luz y algo de materia, pero no es en sí misma luz o materia. La presión que hace explotar un neumático de bicicleta es una interacción entre el aire y el neumático. La presión no es una forma de materia en sí misma. Es tanto una propiedad del neumático como del aire. Análogamente, la hermandad y el empleo son relaciones entre las personas, pero no son personas en sí mismas.
Algunas cosas que parecen ingrávidas sí tienen peso, por lo que califican como materia. El aire tiene peso y, por lo tanto, es una forma de materia a pesar de que una pulgada cúbica de aire pesa menos que un grano de arena. Un globo de helio tiene peso, pero la fuerza del aire más denso que lo rodea evita que caiga. Los astronautas en órbita alrededor de la Tierra tienen peso y caen a lo largo de un arco curvo, pero se mueven tan rápido que el arco curvo de su caída es lo suficientemente amplio como para llevarlos alrededor de la Tierra en un círculo. Se perciben a sí mismos como ingrávidos porque su cápsula espacial se está cayendo junto con ellos y, por lo tanto, el piso no se levanta sobre sus pies.
Tema opcional: Cambios modernos en la definición de luz y materia
Einstein predijo como consecuencia de su teoría de la relatividad que la luz después de todo se vería afectada por gravedad, aunque el efecto sería extremadamente débil en condiciones normales. Su predicción se vio confirmada por las observaciones de la curvatura de los rayos de luz de las estrellas a medida que pasaban cerca del sol en su camino hacia la Tierra. La teoría de Einstein también implicaba la existencia de agujeros negros, estrellas tan masivas y compactas que su gravedad intensa ni siquiera permitiría que la luz escapara. (En estos días existe una fuerte evidencia de que existen agujeros negros).
La interpretación de Einstein fue que la luz realmente no tiene masa, pero que la energía se ve afectada por la gravedad al igual que la masa. La energía en un haz de luz es equivalente a una cierta cantidad de masa, dada por la famosa ecuación (E = mc ^ 2 ), donde (c ) es la velocidad de la luz. Debido a que la velocidad de la luz es un número tan grande, una gran cantidad de energía es equivalente a solo una cantidad muy pequeña de masa, por lo que la fuerza gravitacional en un rayo de luz puede ignorarse para la mayoría de los propósitos prácticos.
Sin embargo, existe una distinción más satisfactoria y fundamental entre la luz y la materia, que debería ser comprensible para usted si ha tenido un curso de química. En química, uno aprende que los electrones obedecen el principio de exclusión de Pauli, que prohíbe que más de un electrón ocupe el mismo orbital si tienen el mismo giro. El principio de exclusión de Pauli es obedecido por las partículas subatómicas de las cuales se compone la materia, pero desobedecidas por las partículas, llamadas fotones, de las cuales se forma un haz de luz.
La teoría de la relatividad de Einstein se analiza con más detalle en el libro 6 de esta serie.
El límite entre la física y las otras ciencias no siempre es claro. Por ejemplo, los químicos estudian los átomos y las moléculas, que son de lo que se construye la materia, y hay algunos científicos que estarían igualmente dispuestos a llamarse químicos físicos o físicos químicos. Puede parecer que la distinción entre física y biología sería más clara, ya que la física parece tratar con objetos inanimados. De hecho, casi todos los físicos estarían de acuerdo en que las leyes básicas de la física que se aplican a las moléculas en un tubo de ensayo funcionan igualmente bien para la combinación de moléculas que constituyen una bacteria. (Algunos podrían creer que algo más sucede en las mentes de los humanos, o incluso en las de los gatos y los perros). Lo que diferencia a la física de la biología es que muchas de las teorías científicas que describen a los seres vivos, a la vez que resultan de las leyes fundamentales de la física, no puede derivarse rigurosamente de principios físicos.
Sistemas aislados y reduccionismo
Para evitar tener que estudiar todo de una vez, los científicos aíslan las cosas que intentan estudiar. Por ejemplo, un físico que quiera estudiar el movimiento de un giroscopio giratorio probablemente preferiría estar aislado de las vibraciones y las corrientes de aire. Incluso en biología, donde el trabajo de campo es indispensable para comprender cómo los seres vivos se relacionan con todo su entorno, es interesante observar el papel histórico vital desempeñado por el estudio de Darwin sobre las Islas Galápagos, que estaban convenientemente aisladas del resto del mundo. Cualquier parte del universo que se considere aparte del resto puede llamarse un “sistema”.
La física ha tenido algunos de sus mayores éxitos al llevar este proceso de aislamiento a los extremos, subdividiendo el universo en partes cada vez más pequeñas. La materia se puede dividir en átomos, y se puede estudiar el comportamiento de los átomos individuales. Los átomos se pueden dividir en sus neutrones, protones y electrones constituyentes. Los protones y los neutrones parecen estar hechos de partículas aún más pequeñas llamadas quarks, e incluso ha habido algunas afirmaciones de evidencia experimental de que los quarks tienen partes más pequeñas dentro de ellos. Este método de dividir las cosas en partes cada vez más pequeñas y estudiar cómo esas partes se influyen entre sí se llama reduccionismo. La esperanza es que las reglas aparentemente complejas que gobiernan las unidades más grandes se puedan entender mejor en términos de reglas más simples que gobiernan las unidades más pequeñas. Para apreciar lo que el reduccionismo ha hecho por la ciencia, solo es necesario examinar un libro de texto de química del siglo XIX. En ese momento, algunos todavía dudaban de la existencia de átomos, ni siquiera se sospechaba que existieran electrones, y casi nada se entendía de qué reglas básicas gobernaban la forma en que los átomos interactuaban entre sí en las reacciones químicas. Los estudiantes tuvieron que memorizar largas listas de productos químicos y sus reacciones, y no había forma de entenderlo sistemáticamente. Hoy, el estudiante solo necesita recordar un pequeño conjunto de reglas sobre cómo interactúan los átomos, por ejemplo, que los átomos de un elemento no pueden convertirse en otro a través de reacciones químicas, o que los átomos del lado derecho de la tabla periódica tienden a formar enlaces fuertes con átomos del lado izquierdo.
Preguntas de discusión
- He sugerido reemplazar la definición ordinaria de diccionario de la luz por una más técnica y más precisa que implique la ingravidez. Sin embargo, todavía es posible que las cosas que hace una bombilla, normalmente llamada “luz”, tengan una pequeña cantidad de peso. Sugiera un experimento para intentar medir si lo hace.
- El calor no tiene peso (es decir, un objeto no se vuelve más pesado cuando se calienta) y puede atravesar una habitación vacía desde la chimenea hasta la piel, donde influye te calentándote ¿Por lo tanto, el calor debe considerarse una forma de luz según nuestra definición? ¿Por qué o por qué no?
- Del mismo modo, ¿el sonido debe considerarse una forma de luz?
0.1.3 Cómo aprender física
Para los conocimientos que ahora se entregan, hay un tipo de contrato de error entre el repartidor y el receptor; porque el que entrega el conocimiento desea entregarlo de la forma que se crea mejor, y no como se pueda examinar mejor; y el que recibe el conocimiento desea más la satisfacción presente que la inquisitiva expectativa. – Francis Bacon
Muchos estudiantes se acercan a un curso de ciencias con la idea de que pueden tener éxito memorizando las fórmulas, de modo que cuando se asigne un problema en la tarea o un examen, poder insertar números en la fórmula y obtener un resultado numérico en su calculadora. ¡Incorrecto! ¡De eso no se trata el aprendizaje de la ciencia! Hay una gran diferencia entre memorizar fórmulas y comprender conceptos. Para empezar, se pueden aplicar diferentes fórmulas en diferentes situaciones. Una ecuación podría representar una definición, que siempre es cierta. Otra podría ser una ecuación muy específica para la velocidad de un objeto deslizándose por un plano inclinado, lo que no sería cierto si el objeto fuera una roca que se desplaza hacia el fondo del océano. Si no trabaja para comprender la física en un nivel conceptual, no sabrá qué fórmulas se pueden usar cuando.
La mayoría de los estudiantes que toman cursos universitarios de ciencias por primera vez también tienen muy poca experiencia con la interpretación del significado de una ecuación. Considere la ecuación (w = A / h ) que relaciona el ancho de un rectángulo con su altura y área. Un estudiante que no ha desarrollado habilidades de interpretación podría ver esto como otra ecuación más para memorizar y conectarse cuando sea necesario. Un estudiante un poco más inteligente podría darse cuenta de que es simplemente la fórmula familiar (A = wh ) en una forma diferente. Cuando se le preguntó si un rectángulo tendría un ancho mayor o menor que otro con la misma área pero una altura menor, el estudiante poco sofisticado podría estar perdido, sin tener ningún número para enchufar en una calculadora. El estudiante más experimentado sabría razonar sobre una ecuación que involucra división — si (h ) es más pequeño y (A ) permanece igual, entonces (w ) debe ser más grande. A menudo, los estudiantes no reconocen una secuencia de ecuaciones como una derivación que conduce a un resultado final, por lo que piensan que todos los pasos intermedios son fórmulas igualmente importantes que deben memorizar.
Al aprender cualquier tema, es importante involucrarse lo más activamente posible, en lugar de tratar de leer toda la información rápidamente sin pensar en ello. Es una buena idea leer y pensar sobre las preguntas que se plantean al final de cada sección de estas notas cuando las encuentre, para que sepa que ha entendido lo que estaba leyendo.
Las dificultades de muchos estudiantes en física se reducen principalmente a dificultades con las matemáticas. Suponga que se siente seguro de que tiene suficiente preparación matemática para tener éxito en este curso, pero está teniendo problemas con algunas cosas específicas. En algunas áreas, la breve revisión dada en este capítulo puede ser suficiente, pero en otras áreas probablemente no lo sea. Una vez que identifique las áreas de matemáticas en las que tiene problemas, obtenga ayuda en esas áreas. No cojees durante todo el curso con un vago sentimiento de temor por algo como la notación científica. El problema no desaparecerá si lo ignora. Lo mismo se aplica a las habilidades matemáticas esenciales que está aprendiendo en este curso por primera vez, como la adición de vectores.
A veces los estudiantes me dicen que siguen tratando de entender un determinado tema en el libro, y simplemente no tiene sentido. Lo peor que puedes hacer en esa situación es seguir mirando la misma página. Cada libro de texto explica mal ciertas cosas, ¡incluso las mías! — así que lo mejor que se puede hacer en esta situación es mirar un libro diferente. En lugar de los libros de texto universitarios destinados al mismo nivel matemático que el curso que está tomando, en algunos casos puede encontrar que los libros de secundaria o los libros en un nivel matemático más bajo dan explicaciones más claras.
Finalmente, cuando revise para un examen, no simplemente lea el texto y sus apuntes. En su lugar, intente utilizar un método activo de revisión, por ejemplo discutiendo algunas de las preguntas de discusión con otro alumno, o haciendo problemas de tarea que no había hecho la primera vez.
0.1.4 Velocidad y aceleración
El cálculo fue inventado por un físico, Isaac Newton, porque lo necesitaba como una herramienta para calcular la velocidad y la aceleración; En su curso introductorio de cálculo, la velocidad y la aceleración probablemente se presentaron como algunas de las primeras aplicaciones.
Si la posición de un objeto en función del tiempo viene dada por la función (x (t) ), entonces su velocidad y aceleración están dadas por las derivadas primera y segunda con respecto al tiempo,
[ begin {align *} v & = frac {dx} {dt} \ text {and} \ a & = frac {d ^ 2 x} {dt ^ 2}. end {align *} ]
La notación se relaciona de manera lógica con las unidades de las cantidades. La velocidad tiene unidades de m / s, y eso tiene sentido porque (dx ) se interpreta como una distancia infinitamente pequeña, con unidades de metros, y (dt ) como un tiempo infinitamente pequeño, con unidades de segundos. La colocación aparentemente extraña e inconsistente de los dos superíndices en la notación para la aceleración también pretende sugerir las unidades: algo en la parte superior con unidades de metros, y algo en la parte inferior con unidades de segundos al cuadrado.
La velocidad y la aceleración tienen interpretaciones físicas completamente diferentes. La velocidad es una cuestión de opinión. En este momento, mientras te sientas en una silla y lees este libro, podrías decir que tu velocidad era cero, pero un observador que observa la rotación de la Tierra diría que tienes una velocidad de cientos de millas por hora. La aceleración representa un cambio en la velocidad, y no es una cuestión de opinión. Las aceleraciones producen efectos físicos, y no ocurren a menos que haya una fuerza para causarlos. Por ejemplo, las fuerzas gravitacionales en la Tierra hacen que los objetos que caen tengan una aceleración de (9.8 text {m} / text {s} ^ 2 ).
| Ejemplo 1: Aceleración constante |
|---|
|
( triangleright ) ¿Qué tan alto debe estar un trampolín sobre el agua para que el buzo tenga hasta 1.0 s en el aire? SOLUCIÓN ( triangleright ) El buzo comienza en reposo y tiene una aceleración de (9.8 text {m} / text {s } ^ 2 ). Necesitamos encontrar una conexión entre la distancia que viaja y el tiempo que toma. En otras palabras, estamos buscando información sobre la función (x (t) ), dada la información sobre la aceleración. Para pasar de la aceleración a la posición, necesitamos integrar dos veces: [ begin {align *} x & = int int a dt dt \ & = int left (at + v_ text {o} right) dt text {[$ v_ text {o} $ es una constante de integración.]} \ & = int en dt text {[$ v_ text {o} $ es cero porque se está cayendo del reposo.]} \ & = frac {1} {2} en ^ 2 + x_ text {o} text {[$ x_ text {o} $ es una constante de integración.]} \ & = frac {1} {2} en ^ 2 text {[$ x_ text {o} $ puede ser cero si lo definimos de esa manera.]} end {align *} ] Tenga en cuenta algunos de los buenos hábitos de resolución de problemas demostrados aquí. Resolvemos el problema simbólicamente, y solo conectamos los números al final, una vez que todo el álgebra y el cálculo están listos. También se debe habituar, después de encontrar un resultado simbólico, a verificar si la dependencia de las variables tiene sentido. Un valor mayor de (t ) en esta expresión conduciría a un valor mayor para (x ); eso tiene sentido, porque si quieres pasar más tiempo en el aire, tendrás que saltar desde más arriba. Una mayor aceleración también conduce a una mayor altura; Esto también tiene sentido, porque cuanto mayor es la gravedad, más altura necesitará para permanecer en el aire durante un período de tiempo determinado. Ahora conectamos los números. [ begin {align *} x & = frac {1} {2} left (9.8 text {m} / text {s} ^ 2 right) (1.0 text {s}) ^ 2 \ & = 4.9 text {m} end {align *} ] Tenga en cuenta que cuando ingresamos los números, verificamos que las unidades funcionen correctamente, ( left ( text {m} / text {s} ^ 2 right) ( text {s}) ^ 2 = text {m} ). También debemos verificar que el resultado tenga sentido: 4,9 metros es bastante alto, pero no es irrazonable. |
La notación (dq ) en el cálculo representa un cambio infinitesimalmente pequeño en la variable (q ). La notación correspondiente para un cambio finito en una variable es ( Delta q ). Por ejemplo, si (q ) representa el valor de una determinada acción en el mercado de valores, y el valor cae de (q_ text {o} = 5 ) dólares inicialmente a (q_f = 3 ) dólares finalmente , entonces ( Delta q = -2 ) dólares. Cuando estudiamos funciones lineales, cuyas pendientes son constantes, la derivada es sinónimo de la pendiente de la línea, y (dy / dx ) es lo mismo que ( Delta y / Delta x ), el aumento sobre la carrera.
En condiciones de aceleración constante, podemos relacionar la velocidad y el tiempo,
[ begin {ecation *} a = frac { Delta v} { Delta t}, end {ecuación *} ]
o, como en el ejemplo 1 , posición y tiempo,
[ begin {ecation *} x = frac {1 } {2} en ^ 2 + v_ text {o} t + x_ text {o}. end {ecuación *} ]
También puede ser útil tener una relación que involucre velocidad y posición, eliminando el tiempo. Álgebra directa da
[ begin {ecation *} v_f ^ 2 = v_ text {o} ^ 2 + 2 a Delta x, end {ecation *} ]
donde (v_f ) es la velocidad final, (v_ text {o} ) la velocidad inicial y ( Delta x ) la distancia recorrida.
- Problema resuelto: Dejar caer una roca sobre Marte – problema 17
- Problema resuelto: La Dodge Viper – problema 19
0.1.5 Autoevaluación
La parte introductoria de un libro como este es difícil de escribir, porque cada estudiante llega a este punto de partida con una preparación diferente. Un estudiante puede haber crecido fuera de los EE. UU. Y, por lo tanto, puede sentirse completamente cómodo con el sistema métrico, pero puede haber tenido un curso de álgebra en el que el instructor pasó demasiado rápido sobre la notación científica. Es posible que otro estudiante ya haya tomado cálculo vectorial, pero puede que nunca haya aprendido el sistema métrico. The following self-evaluation is a checklist to help you figure out what you need to study to be prepared for the rest of the course.
|
If you disagree with this statement … |
you should study this section: |
|
I am familiar with the basic metric units of meters, kilograms, and seconds, and the most common metric prefixes: milli- (m), kilo- (k), and centi- (c). |
subsection 0.1.6 Basic of the Metric System |
|
I am familiar with these less common metric prefixes: mega- (M), micro- μ), and nano- (n). |
subsection 0.1.7 Less Common Metric Prefixes |
|
I am comfortable with scientific notation. |
subsection 0.1.8 Scientific Notation |
|
I can confidently do metric conversions. |
subsection 0.1.9 Conversions |
|
I understand the purpose and use of significant figures. |
subsection 0.1.10 Significant Figures |
It wouldn’t hurt you to skim the sections you think you already know about, and to do the self-checks in those sections.
The metric system
Units were not standardized until fairly recently in history, so when the physicist Isaac Newton gave the result of an experiment with a pendulum, he had to specify not just that the string was 37 (^7/_8) inches long but that it was “37 (^7/_8) London inches long.” The inch as defined in Yorkshire would have been different. Even after the British Empire standardized its units, it was still very inconvenient to do calculations involving money, volume, distance, time, or weight, because of all the odd conversion factors, like 16 ounces in a pound, and 5280 feet in a mile. Through the nineteenth century, schoolchildren squandered most of their mathematical education in preparing to do calculations such as making change when a customer in a shop offered a one-crown note for a book costing two pounds, thirteen shillings and tuppence. The dollar has always been decimal, and British money went decimal decades ago, but the United States is still saddled with the antiquated system of feet, inches, pounds, ounces and so on.
Every country in the world besides the U.S. uses a system of units known in English as the “metric system. 1 ” This system is entirely decimal, thanks to the same eminently logical people who brought about the French Revolution. In deference to France, the system’s official name is the Système International, or SI, meaning International System. (The phrase “SI system” is therefore redundant.)
The wonderful thing about the SI is that people who live in countries more modern than ours do not need to memorize how many ounces there are in a pound, how many cups in a pint, how many feet in a mile, etc. The whole system works with a single, consistent set of Greek and Latin prefixes that modify the basic units. Each prefix stands for a power of ten, and has an abbreviation that can be combined with the symbol for the unit. For instance, the meter is a unit of distance. The prefix kilo- stands for (10^3), so a kilometer, 1 km, is a thousand meters.
The basic units of the metric system are the meter for distance, the second for time, and the gram for mass.
The following are the most common metric prefixes. You should memorize them.
| prefix | meaning | example | ||
| kilo- | k | 10 3 | 60 kg |
= a person’s mass |
| centi- | c | 10 −2 | 28 cm |
= height of a piece of paper |
| milli- | m | 10 −3 | 1 ms |
= time for one vibration of a guitar string playing the note D |
The prefix centi-, meaning (10^{-2}), is only used in the centimeter; a hundredth of a gram would not be written as 1 cg but as 10 mg. The centi- prefix can be easily remembered because a cent is (10^{-2}) dollars. The official SI abbreviation for seconds is “s” (not “sec”) and grams are “g” (not “gm”).
The second
When I stated briefly above that the second was a unit of time, it may not have occurred to you that this was not much of a definition. We can make a dictionary-style definition of a term like “time,” or give a general description like Isaac Newton’s: “Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external…” Newton’s characterization sounds impressive, but physicists today would consider it useless as a definition of time. Today, the physical sciences are based on operational definitions, which means definitions that spell out the actual steps (operations) required to measure something numerically.
In an era when our toasters, pens, and coffee pots tell us the time, it is far from obvious to most people what is the fundamental operational definition of time. Until recently, the hour, minute, and second were defined operationally in terms of the time required for the earth to rotate about its axis. Unfortunately, the Earth’s rotation is slowing down slightly, and by 1967 this was becoming an issue in scientific experiments requiring precise time measurements. The second was therefore redefined as the time required for a certain number of vibrations of the light waves emitted by a cesium atoms in a lamp constructed like a familiar neon sign but with the neon replaced by cesium. The new definition not only promises to stay constant indefinitely, but for scientists is a more convenient way of calibrating a clock than having to carry out astronomical measurements.
self-check:
What is a possible operational definition of how strong a person is?
(answer in the back of the PDF version of the book)
The meter
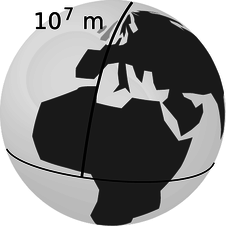
e / The original definition of the meter.
The French originally defined the meter as (10^{-7}) times the distance from the equator to the north pole, as measured through Paris (of course). Even if the definition was operational, the operation of traveling to the north pole and laying a surveying chain behind you was not one that most working scientists wanted to carry out. Fairly soon, a standard was created in the form of a metal bar with two scratches on it. This was replaced by an atomic standard in 1960, and finally in 1983 by the current definition, which is that the meter is the distance traveled by light in a vacuum over a period of (1/299792458) seconds.
The kilogram
The third base unit of the SI is the kilogram, a unit of mass. Mass is intended to be a measure of the amount of a substance, but that is not an operational definition. Bathroom scales work by measuring our planet’s gravitational attraction for the object being weighed, but using that type of scale to define mass operationally would be undesirable because gravity varies in strength from place to place on the earth.
There’s a surprising amount of disagreement among physics textbooks about how mass should be defined, but here’s how it’s actually handled by the few working physicists who specialize in ultra-high-precision measurements. They maintain a physical object in Paris, which is the standard kilogram, a cylinder made of platinum-iridium alloy. Duplicates are checked against this mother of all kilograms by putting the original and the copy on the two opposite pans of a balance. Although this method of comparison depends on gravity, the problems associated with differences in gravity in different geographical locations are bypassed, because the two objects are being compared in the same place. The duplicates can then be removed from the Parisian kilogram shrine and transported elsewhere in the world. It would be desirable to replace this at some point with a universally accessible atomic standard rather than one based on a specific artifact, but as of 2010 the technology for automated counting of large numbers of atoms has not gotten good enough to make that work with the desired precision.

f / A duplicate of the Paris kilogram, maintained at the Danish National Metrology Institute.
Combinations of metric units
Just about anything you want to measure can be measured with some combination of meters, kilograms, and seconds. Speed can be measured in m/s, volume in (text{m}^3), and density in (text{kg}/text{m}^3). Part of what makes the SI great is this basic simplicity. No more funny units like a cord of wood, a bolt of cloth, or a jigger of whiskey. No more liquid and dry measure. Just a simple, consistent set of units. The SI measures put together from meters, kilograms, and seconds make up the mks system. For example, the mks unit of speed is m/s, not km/hr.
Checking units
A useful technique for finding mistakes in one’s algebra is to analyze the units associated with the variables.
| Example 2: Checking Units |
|---|
|
(triangleright) Jae starts from the formula (V=frac{1}{3}Ah) for the volume of a cone, where (A) is the area of its base, and (h) is its height. He wants to find an equation that will tell him how tall a conical tent has to be in order to have a certain volume, given its radius. His algebra goes like this: [begin{align*} V &= frac{1}{3}Ah \ A &= pi r^2 \ V &= frac{1}{3}pi r^2 h\ h &= frac{pi r^2}{3V} end{align*}] Is his algebra correct? If not, find the mistake. (triangleright) Line 4 is supposed to be an equation for the height, so the units of the expression on the right-hand side had better equal meters. The pi and the 3 are unitless, so we can ignore them. In terms of units, line 4 becomes [begin{equation*} text{m} = frac{text{m}^2}{text{m}^3} = frac{1}{text{m}} . end{equation*}] This is false, so there must be a mistake in the algebra. The units of lines 1, 2, and 3 check out, so the mistake must be in the step from line 3 to line 4. In fact the result should have been [begin{equation*} h = frac{3V}{pi r^2} . end{equation*}] Now the units check: (text{m} = text{m}^3/text{m}^2). |
Discussion Question
Isaac Newton wrote, “… the natural days are truly unequal, though they are commonly considered as equal, and used for a measure of time… It may be that there is no such thing as an equable motion, whereby time may be accurately measured. All motions may be accelerated or retarded…” Newton was right. Even the modern definition of the second in terms of light emitted by cesium atoms is subject to variation. For instance, magnetic fields could cause the cesium atoms to emit light with a slightly different rate of vibration. What makes us think, though, that a pendulum clock is more accurate than a sundial, or that a cesium atom is a more accurate timekeeper than a pendulum clock? That is, how can one test experimentally how the accuracies of different time standards compare?
0.1.7 Less common metric prefixes
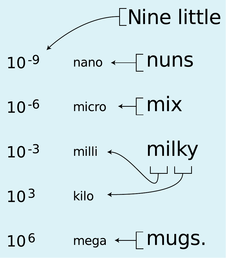
g / This is a mnemonic to help you remember the most important metric prefixes. The word “little” is to remind you that the list starts with the prefixes used for small quantities and builds upward. The exponent changes by 3, except that of course that we do not need a special prefix for (10^0), which equals one.
The following are three metric prefixes which, while less common than the ones discussed previously, are well worth memorizing.
| prefix | meaning | example | ||
| mega- | M 10 6 | 6.4 Mm | = radius of the earth | |
| micro- | μ 10 −6 | 10 µ m | = size of a white blood cell | |
| nano- | n 10 −9 | 0.154 nm | = distance between carbon nuclei in an ethane molecule | |
Note that the abbreviation fo r micro is the Greek letter mu, (mu) — a common mistake is to confuse it with m (milli) or M (mega).
There are other prefixes even less common, used for extremely large and small quantities. For instance, (1 text{femtometer}=10^{-15} text{m}) is a convenient unit of distance in nuclear physics, and (1 text{gigabyte}=10^9) bytes is used for computers’ hard disks. The international committee that makes decisions about the SI has recently even added some new prefixes that sound like jokes, e.g., (1 text{yoctogram}=10^{-24} text{g}) is about half the mass of a proton. In the immediate future, however, you’re unlikely to see prefixes like “yocto-” and “zepto-” used except perhaps in trivia contests at science-fiction conventions or other geekfests.
self-check:
Suppose you could slow down time so that according to your perception, a beam of light would move across a room at the speed of a slow walk. If you perceived a nanosecond as if it was a second, how would you perceive a microsecond?
(answer in the back of the PDF version of the book)
0.1.8 Scientific notation
Most of the interesting phenomena in our universe are not on the human scale. It would take about 1,000,000,000,000,000,000,000 bacteria to equal the mass of a human body. When the physicist Thomas Young discovered that light was a wave, it was back in the bad old days before scientific notation, and he was obliged to write that the time required for one vibration of the wave was 1/500 of a millionth of a millionth of a second. Scientific notation is a less awkward way to write very large and very small numbers such as these. Here’s a quick review.
Scientific notation means writing a number in terms of a product of something from 1 to 10 and something else that is a power of ten. For instance,
[begin{align*} & 32 = 3.2 times 10^1\ & 320 = 3.2 times 10^2\ & 3200 = 3.2 times 10^3 … end{align*}]
Each number is ten times bigger than the previous one.
Since (10^1) is ten times smaller than (10^2) , it makes sense to use the notation (10^0) to stand for one, the number that is in turn ten times smaller than (10^1) . Continuing on, we can write (10^{-1}) to stand for 0.1, the number ten times smaller than (10^0) . Negative exponents are used for small numbers:
[begin{align*} &3.2 = 3.2 times 10^0\ &0.32 = 3.2 times 10^{-1}\ &0.032 = 3.2 times 10^{-2} … end{align*}]
A common source of confusion is the notation used on the displays of many calculators. Examples:
| 3.2×10 6 | (written notation) |
| 3.2E+6 | (notation on some calculators) |
| 3.2 6 | (notation on some other calculators) |
The last example is particularly unfortunate, because (3.2^6) really stands for the number (3.2 times 3.2 times 3.2 times 3.2 times 3.2 times 3.2= 1074), a totally different number from (3.2 times 10^6=3200000). The calculator notation should never be used in writing. It’s just a way for the manufacturer to save money by making a simpler display.
self-check:
A student learns that (10^4) bacteria, standing in line to register for classes at Paramecium Community College, would form a queue of this size:

The student concludes that (10^2) bacteria would form a line of this length:

Why is the student incorrect?
(answer in the back of the PDF version of the book)
0.1.9 Conversions
Conversions are one of the three essential mathematical skills, summarized on pp.905-907, that you need for success in this course.
I suggest you avoid memorizing lots of conversion factors between SI units and U.S. units, but two that do come in handy are:
1 inch = 2.54 cm
An object with a weight on Earth of 2.2 pounds-force has a mass of 1 kg.
The first one is the present definition of the inch, so it’s exact. The second one is not exact, but is good enough for most purposes. (U.S. units of force and mass are confusing, so it’s a good thing they’re not used in science. In U.S. units, the unit of force is the pound-force, and the best unit to use for mass is the slug, which is about 14.6 kg.)
More important than memorizing conversion factors is understanding the right method for doing conversions. Even within the SI, you may need to convert, say, from grams to kilograms. Different people have different ways of thinking about conversions, but the method I’ll describe here is systematic and easy to understand. The idea is that if 1 kg and 1000 g represent the same mass, then we can consider a fraction like
[begin{equation*} frac{10^3 text{g}}{1 text{kg}} end{equation*}]
to be a way of expressing the number one. This may bother you. For instance, if you type 1000/1 into your calculator, you will get 1000, not one. Again, different people have different ways of thinking about it, but the justification is that it helps us to do conversions, and it works! Now if we want to convert 0.7 kg to units of grams, we can multiply kg by the number one:
[begin{equation*} 0.7 text{kg} times frac{10^3 text{g}}{1 text{kg}} end{equation*}]
If you’re willing to treat symbols such as “kg” as if they were variables as used in algebra (which they’re really not), you can then cancel the kg on top with the kg on the bottom, resulting in
[begin{equation*} 0.7 {text{kg}} times frac{10^3 text{g}}{1 {text{kg}}} = 700 text{g} . end{equation*}]
To convert grams to kilograms, you would simply flip the fraction upside down.
One advantage of this method is that it can easily be applied to a series of conversions. For instance, to convert one year to units of seconds,
[begin{multline*} 1 {text{year}} times frac{365 {text{days}}}{1 {text{year}}} times frac{24 {text{hours}}}{1 {text{day}}} times frac{60 {text{min}}}{1 {text{hour}}} times frac{60 text{s}}{1 {text{min}}} = 3.15 times 10^7 text{s} . end{multline*}]
Should that exponent be positive, or negative?
A common mistake is to write the conversion fraction incorrectly. For instance the fraction
[begin{equation*} frac{10^3 text{kg}}{1 text{g}} text{(incorrect)} end{equation*}]
does not equal one, because (10^3) kg is the mass of a car, and 1 g is the mass of a raisin. One correct way of setting up the conversion factor would be
[begin{equation*} frac{10^{-3} text{kg}}{1 text{g}} text{(correct)} . end{equation*}]
You can usually detect such a mistake if you take the time to check your answer and see if it is reasonable.
If common sense doesn’t rule out either a positive or a negative exponent, here’s another way to make sure you get it right. There are big prefixes and small prefixes:
| big prefixes: | k M |
| small prefixes: | m μ n |
(It’s not hard to keep straight which are which, since “mega” and “micro” are evocative, and it’s easy to remember that a kilometer is bigger than a meter and a millimeter is smaller.) In the example above, we want the top of the fraction to be the same as the bottom. Since (k) is a big prefix, we need to compensate by putting a small number like (10^{-3}) in front of it, not a big number like (10^3).
- Solved problem: a simple conversion — problem 6
- Solved problem: the geometric mean — problem 8
Discussion Question
Each of the following conversions contains an error. In each case, explain what the error is.
- (1000 text{kg} times frac{1 text{kg}}{1000 text{g}} = 1 text{g})
- (50 text{m} times frac{1 text{cm}}{100 text{m}} = 0.5 text{cm})
- “Nano” is (10^{-9}), so there are (10^{-9}) nm in a meter.
- “Micro” is (10^{-6}), so 1 kg is (10^6 mutext{g}).
0.1.10 Significant figures
An engineer is designing a car engine, and has been told that the diameter of the pistons (which are being designed by someone else) is 5.0 cm. He knows that 0.02 cm of clearance is required for a piston of this size, so he designs the cylinder to have an inside diameter of 5.02 cm. Luckily, his supervisor catches his mistake before the car goes into production. She explains his error to him, and mentally puts him in the “do not promote” category.
What was his mistake? The person who told him the diameter of the piston intentionally said “5.0 cm,” not “5.00 cm,” specifically to avoid creating the impression that the number was extremely accurate. In reality, the piston’s diameter was 5.04 cm. They would never have fit in the 5.02 cm cylinders.
In most cases, the result of a calculation involving several pieces of data can be no more accurate than the least accurate piece of data. “Garbage in, garbage out.” Since the 5.0 cm figure for the diameter of the pistons was not very accurate, the result of the engineer’s calculation, 5.04 cm, was really not as accurate as he thought.
For calculations involving multiplication and division, a given fractional or “percent” error in one of the inputs causes the same fractional error in the output. The number of digits in a number provides a rough measure of its possible fractional error. These are called significant figures or “sig figs.” Examples:
| 3.14 |
3 sig figs |
| 3.1 |
2 sig figs |
| 0.03 |
1 sig fig, because the zeroes are just placeholders |
| 3.0×10 1 |
2 sig figs |
| 30 |
could be 1 or 2 sig figs, since we can’t tell if the 0 is a placeholder or a real sig fig |
In such calculations, your result should not have more than the number of sig fi gs in the least accurate piece of data you started with.
| Example 3: Sig figs in the area of a triangle |
|---|
|
(triangleright) A triangle has an area of (6.45 text{m}^2) and a base with a width of (4.0138 text{m}). Find its height. (triangleright) The area is related to the base and height by (A=bh/2). [begin{align*} h &= frac{2A}{b} \ &= 3.21391200358762 text{m}quad text{(calculator output)} \ &= 3.21 text{m} end{align*}] The given data were 3 sig figs and 5 sig figs. We’re limited by the less accurate piece of data, so the final result is 3 sig figs. The additional digits on the calculator don’t mean anything, and if we communicated them to another person, we would create the false impression of having determined (h) with more precision than we really obtained. |
self-check:
The following quote is taken from an editorial by Norimitsu Onishi in the New York Times, August 18, 2002.
Consider Nigeria. Everyone agrees it is Africa’s most populous nation. But what is its population? The United Nations says 114 million; the State Department, 120 million. The World Bank says 126.9 million, while the Central Intelligence Agency puts it at 126,635,626.
What should bother you about this?
(answer in the back of the PDF version of the book)
Dealing correctly with significant figures can save you time! Often, students copy down numbers from their calculators with eight significant figures of precision, then type them back in for a later calculation. That’s a waste of time, unless your original data had that kind of incredible precision.
self-check:
How many significant figures are there in each of the following measurements?
(1) 9.937 m
(2) 4.0 s
(3) 0.0000000000000037 kg
(answer in the back of the PDF version of the book)
The rules about significant figures are only rules of thumb, and are not a substitute for careful thinking. For instance, $20.00 + $0.05 is $20.05. It need not and should not be rounded off to $20. In general, the sig fig rules work best for multiplication and division, and we sometimes also apply them when doing a complicated calculation that involves many types of operations. For simple addition and subtraction, it makes more sense to maintain a fixed number of digits after the decimal point.
When in doubt, don’t use the sig fig rules at all. Instead, intentionally change one piece of your initial data by the maximum amount by which you think it could have been off, and recalculate the final result. The digits on the end that are completely reshuffled are the ones that are meaningless, and should be omitted.
| Example 4: A nonlinear function |
|---|
|
(triangleright) How many sig figs are there in (sin 88.7°)? SOLUTION (triangleright) We’re using a sine function, which isn’t addition, subtraction, multiplication, or division. It would be reasonable to guess that since the input angle had 3 sig figs, so would the output. But if this was an important calculation and we really needed to know, we would do the following: [begin{align*} sin 88.7° &= 0.999742609322698 \ sin 88.8° &= 0.999780683474846 end{align*}] Surprisingly, the result appears to have as many as 5 sig figs, not just 3: [begin{equation*} sin 88.7° = 0.99974 , end{equation*}] where the final 4 is uncertain but may have some significance. The unexpectedly high precision of the result is because the sine function is nearing its maximum at 90 degrees, where the graph flattens out and becomes insensitive to the input angle. |